题目内容
12.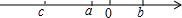 实数a、b、c在数轴上的位置如图所示,则$\sqrt{(a-b)^{2}}$-|a+c|+$\sqrt{(c-b)^{2}}$-|-b|=b.
实数a、b、c在数轴上的位置如图所示,则$\sqrt{(a-b)^{2}}$-|a+c|+$\sqrt{(c-b)^{2}}$-|-b|=b.
分析 先根据实数a、b、c在数轴上的位置,得出a-b<0,a+c<0,c-b<0,-b<0,再根据二次根式的性质进行求解即可.
解答 解:根据实数a、b、c在数轴上的位置,可得出:
a-b<0,a+c<0,c-b<0,-b<0,
∴原式=|a-b|-|a+c|+|c-b|-|-b|
=-(a-b)+(a+c)-(c-b)+(-b)
=b-a+a+c-c+b-b
=b.
故答案为:b.
点评 本题考查了二次根式的性质与化简,解答本题的关键在于根据实数a、b、c在数轴上的位置,得出a-b<0,a+c<0,c-b<0,-b<0,再根据二次根式的性质进行求解.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案 天天练口算系列答案
天天练口算系列答案
相关题目
20. 为进一步缓解城市交通压力,湖州推出公共自行车.公共自行车在任何一个网店都能实现通租通还,某校学生小明统计了周六校门口停车网点各时段的借、还自行车数,以及停车点整点时刻的自行车总数(称为存量)情况,表格中x=1时的y的值表示8:00点时的存量,x=2时的y值表示9:00点时的存量…以此类推,他发现存量y(辆)与x(x为整数)满足如图所示的一个二次函数关系.
为进一步缓解城市交通压力,湖州推出公共自行车.公共自行车在任何一个网店都能实现通租通还,某校学生小明统计了周六校门口停车网点各时段的借、还自行车数,以及停车点整点时刻的自行车总数(称为存量)情况,表格中x=1时的y的值表示8:00点时的存量,x=2时的y值表示9:00点时的存量…以此类推,他发现存量y(辆)与x(x为整数)满足如图所示的一个二次函数关系.
根据所给图表信息,解决下列问题:
(1)m=13,解释m的实际意义:7:00时自行车的存量;
(2)求整点时刻的自行车存量y与x之间满足的二次函数关系式;
(3)已知10:00-11:00这个时段的还车数比借车数的2倍少4,求此时段的借车数.
 为进一步缓解城市交通压力,湖州推出公共自行车.公共自行车在任何一个网店都能实现通租通还,某校学生小明统计了周六校门口停车网点各时段的借、还自行车数,以及停车点整点时刻的自行车总数(称为存量)情况,表格中x=1时的y的值表示8:00点时的存量,x=2时的y值表示9:00点时的存量…以此类推,他发现存量y(辆)与x(x为整数)满足如图所示的一个二次函数关系.
为进一步缓解城市交通压力,湖州推出公共自行车.公共自行车在任何一个网店都能实现通租通还,某校学生小明统计了周六校门口停车网点各时段的借、还自行车数,以及停车点整点时刻的自行车总数(称为存量)情况,表格中x=1时的y的值表示8:00点时的存量,x=2时的y值表示9:00点时的存量…以此类推,他发现存量y(辆)与x(x为整数)满足如图所示的一个二次函数关系.| 时段 | x | 还车数 | 借车数 | 存量y |
| 7:00-8:00 | 1 | 7 | 5 | 15 |
| 8:00-9:00 | 2 | 8 | 7 | n |
| … | … | … | … | … |
(1)m=13,解释m的实际意义:7:00时自行车的存量;
(2)求整点时刻的自行车存量y与x之间满足的二次函数关系式;
(3)已知10:00-11:00这个时段的还车数比借车数的2倍少4,求此时段的借车数.
 已知一次函数y=kx+b的图象如图所示:
已知一次函数y=kx+b的图象如图所示: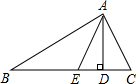 如图,已知△ABC中,AE是∠CAB的平分线,AD是高,∠B=30°,∠C=50°,求
如图,已知△ABC中,AE是∠CAB的平分线,AD是高,∠B=30°,∠C=50°,求 已知△ABN和△ACM位置如图所示,AB=AC,∠1=∠2,∠M=∠N.求证:AD=AE.
已知△ABN和△ACM位置如图所示,AB=AC,∠1=∠2,∠M=∠N.求证:AD=AE.