题目内容
8.一次函数$y=\frac{1}{2}x-2$的图象与x轴交点是(4,0),与y轴的交点是(0,-2),图象与x,y轴所围的三角形的面积是4.分析 根据坐标轴上点的坐标特征求出直线与x轴和y轴的交点坐标,然后根据三角形面积公式计算图象与坐标轴所围成的三角形面积.
解答 解:当y=0时,0.5x-2=0,解得x=4,所以直线与x轴交点坐标是(4,0),
当x=0时,y=0.5x-2=-2,所以直线与y轴交点坐标是(0,-2),
所以图象与坐标轴所围成的三角形面积=$\frac{1}{2}$×4×2=4.
故答案为(4,0),(0,-2),4.
点评 本题考查了一次函数图象上点的坐标特征:一次函数y=kx+b,(k≠0,且k,b为常数)的图象是一条直线.它与x轴的交点坐标是(-$\frac{b}{k}$,0);与y轴的交点坐标是(0,b).直线上任意一点的坐标都满足函数关系式y=kx+b.

练习册系列答案
相关题目
18.用代数式表示“a的平方的2倍与b的差的一半”为( )
| A. | $\frac{1}{2}$(2a-b0 | B. | $\frac{1}{2}$(2a2-b) | C. | 2a2-$\frac{1}{2}$b | D. | (2a)2-$\frac{1}{2}$b |
3.在下列各组中,表示互为相反意义的量是( )
| A. | 上升与下降 | B. | 篮球比赛胜5场与负2场 | ||
| C. | 向东走3米,再向南走3米 | D. | 增产10吨粮食与减产-10吨粮食 |
18.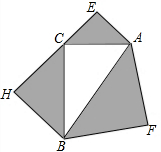 如图,以△ABC的三边为邻边分别向外作等腰直角三角形,且S△AFB=169,S△AEC=25,S△CHB=144,则S△ACB=( )
如图,以△ABC的三边为邻边分别向外作等腰直角三角形,且S△AFB=169,S△AEC=25,S△CHB=144,则S△ACB=( )
 如图,以△ABC的三边为邻边分别向外作等腰直角三角形,且S△AFB=169,S△AEC=25,S△CHB=144,则S△ACB=( )
如图,以△ABC的三边为邻边分别向外作等腰直角三角形,且S△AFB=169,S△AEC=25,S△CHB=144,则S△ACB=( )| A. | 130 | B. | 120 | C. | 100 | D. | 90 |
 按下列要求作图.
按下列要求作图.