题目内容
17.二次函数y=x2+x-2与x轴交于点(-2,0),(1,0),与y轴交于点(0,-2).(填点的坐标)分析 根据抛物线与x轴的交点问题,通过解方程x2+x-2=0可得到二次函数图象与x轴的交点坐标,然后计算自变量为0时的函数值可确定二次函数图象与y轴的交点坐标.
解答 解:当y=0时,x2+x-2=0,解得x1=-2,x2=1,则二次函数图象与x轴的交点坐标为(-2,0),(1,0);
当x=0时,y=x2+x-2=-2,则二次函数图象与y轴的交点坐标为(0,-2).
故答案为(-2,0),(1,0);(0,-2).
点评 本题考查了抛物线与x轴的交点:把求二次函数y=ax2+bx+c(a,b,c是常数,a≠0)与x轴的交点坐标问题转化为解关于x的一元二次方程问题.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案
相关题目
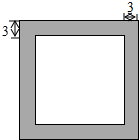 一标志性建筑的底面呈正方形,在其四周铺上花岗石,形成一个边宽为3米的正方形框(如图所示中阴影部分)已知铺这个框恰好用了192块边长为0.75米的正方形花岗石(接缝忽略不计),问标志性建筑底面的边长是多少米?
一标志性建筑的底面呈正方形,在其四周铺上花岗石,形成一个边宽为3米的正方形框(如图所示中阴影部分)已知铺这个框恰好用了192块边长为0.75米的正方形花岗石(接缝忽略不计),问标志性建筑底面的边长是多少米?