Question

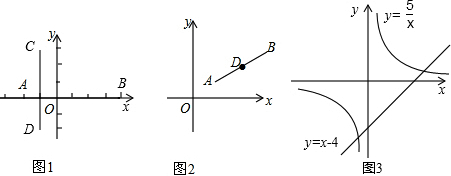
2．问题1：在图1中，已知线段AB，CD，它们的中点分别为E，F．
①若A（-2，0），B（4，0），则E点坐标为（1，0）；
②若C（-1，3），D（-1，-2），则F点坐标为（-1，$\frac{1}{2}$）；
问题2：在图2中，无论线段AB处于直角坐标系中的哪个位置，当其端点坐标为A（a，b），B（c，d），AB中点为D（x，y）时，请直接写出D点的坐标（$\frac{a+c}{2}$，$\frac{b+d}{2}$）；（用含a、b、c、d的式子表示）．
问题3：如图3，一次函数y=x-4与反比例函数y=$\frac{5}{x}$的图象交于A、B两点，若以A、O、B、P为顶点的四边形是平行四边形，请直接写出顶点P的坐标（4，-4）或（6，6）或（-6，-6）．

Answer 1

分析 问题1：中①②正确作出两线段的中点，即可写出中点的坐标；
问题2：过点A，D，B三点分别作x轴的垂线，垂足分别为A'，D'，B'，则AA'∥BB'∥DD'，根据梯形中位线定理即可得到D点坐标；
问题3：根据A，B两点坐标，根据上面的结论可以求得AB的中点的坐标，此点也是OP的中点，根据前边的结论即可求解．

解答 解：
问题1：
①∵A（-2，0），B（4，0），
∴线段AB的中点坐标为（$\frac{-2+4}{2}$，0），即（1，0），
∴E点坐标为（1，0）；
②∵C（-1，3），D（-1，-2），
∴线段CD的中点坐标为（$\frac{-1+（-1）}{2}$，$\frac{3+（-2）}{2}$），即（-1，$\frac{1}{2}$），
∴F点坐标为（-1，$\frac{1}{2}$）；
问题2：
如图，过点A，D，B三点分别作x轴的垂线，垂足分别为A′，D′，B′，则AA′∥BB′∥CC′，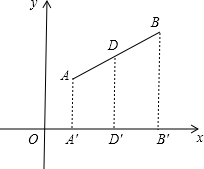

∵D为AB中点，由平行线分线段成比例定理得，A′D′=D′B′，
∴OD′=a+$\frac{c-a}{2}$=$\frac{a+c}{2}$，
即D点的横坐标是$\frac{a+c}{2}$，
同理可得D点的纵坐标是$\frac{b+d}{2}$，
∴AB中点D的坐标为（$\frac{a+c}{2}$，$\frac{b+d}{2}$）；
问题3：
由题意得$\left\{\begin{array}{l}{y=x-4}\\{y=\frac{5}{x}}\end{array}\right.$，
解得$\left\{\begin{array}{l}{x=5}\\{y=1}\end{array}\right.$或$\left\{\begin{array}{l}{x=-1}\\{y=-5}\end{array}\right.$，
∴即交点的坐标为A（-1，-5），B（5，1），
以AB为对角线时，由上面的结论知AB中点M的坐标为（2，-2），
∵平行四边形对角线互相平分，
∴OM=OP，即M为OP的中点，
∴P点坐标为（4，-4），
同理可得分别以OA，OB为对角线时，点P坐标分别为（6，6），（-6，-6），
∴满足条件的点P有三个，坐标分别是（4，-4），（6，6），（-6，-6）．
故答案为：（1，0）；（-1，$\frac{1}{2}$）；（$\frac{a+c}{2}$，$\frac{b+d}{2}$）；（4，-4）或（6，6）或（-6，-6）．

点评 本题主要考查反比例函数的综合，涉及中点坐标公式、梯形中位线定理、函数图象交点和平行四边形的性质等知识点．在问题1中注意确定出两线段的中点的位置，在问题2中把A、B、D转化到x轴上，利用梯形的中位线定理是解题的关键，在问题3中注意利用前面的结论．本题所考查知识比较基础，注重了知识的探究和运用，难度不大．