题目内容
12.已知x2-3x+1=0,求代数式($\frac{x}{x-1}$-$\frac{x-1}{x+1}$)÷$\frac{{x}^{2}}{{x}^{2}-1}$的值.分析 先根据分式混合运算的法则把原式进行化简,再根据x2-3x+1=0得出x2=3x-1,代入原式进行计算即可.
解答 解:原式=$\frac{x(x+1)-(x-1)^{2}}{(x+1)(x-1)}$•$\frac{(x+1)(x-1)}{{x}^{2}}$
=$\frac{3x-1}{(x+1)(x-1)}$•$\frac{(x+1)(x-1)}{{x}^{2}}$
=$\frac{3x-1}{{x}^{2}}$,
又∵x2-3x+1=0,
∴x2=3x-1,
∴原式=1.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
1. 如图,已知AC∥BD,∠B=70°,AE平分∠BAC,则∠1的度数为( )
如图,已知AC∥BD,∠B=70°,AE平分∠BAC,则∠1的度数为( )
 如图,已知AC∥BD,∠B=70°,AE平分∠BAC,则∠1的度数为( )
如图,已知AC∥BD,∠B=70°,AE平分∠BAC,则∠1的度数为( )| A. | 60° | B. | 50° | C. | 55° | D. | 70° |
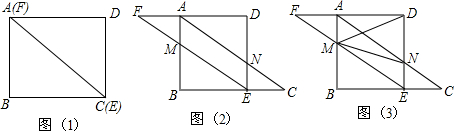
 如图所示,折叠矩形的一边AD,使点D落在BC上的点F处,已知:AB=8cm,BC=10cm.求EC的长.
如图所示,折叠矩形的一边AD,使点D落在BC上的点F处,已知:AB=8cm,BC=10cm.求EC的长. 在平面直角坐标系中,三角形ABC的边AB在x轴上,且AB=3,已知点A的坐标为(2,0),顶点C的坐标为(-2,4).
在平面直角坐标系中,三角形ABC的边AB在x轴上,且AB=3,已知点A的坐标为(2,0),顶点C的坐标为(-2,4).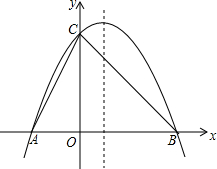 如图,已知抛物线y=ax2-2ax+4与x轴交于A、B两点,与y轴交于点C,且OB=OC.
如图,已知抛物线y=ax2-2ax+4与x轴交于A、B两点,与y轴交于点C,且OB=OC. 如图所示的图形是由8个完全相同的小正方体组成的立体图形,则这个几何体的俯视图是( )
如图所示的图形是由8个完全相同的小正方体组成的立体图形,则这个几何体的俯视图是( )