题目内容
7.方程x2-y2=2010的整数解的组数为12.分析 由平方差公式可知x2-y2=(x+y)(x-y),(x+y)与 (x-y)是奇数或者偶数,将2010分为两个数的积,分别解方程组即可.
解答 解:∵2010=1×2010=(-1)×(-2010)=10×201=(-10)×(-201)=(2)×(1005)=(-2)×(-1005),
∴(x+y),(x-y)分别可取下列数对
(1,2010),(2010,1),(-1,-2010),(-2010,-1),
(10,201),(201,10),(-10,-201),(-201,-10),
(2,1005)、(-2,-1005)、(1005,2)、(-1005,-2),
由此可得方程有12组整数解.
故答案为12
点评 本题主要考查非一次不定方程的知识点,解答本题的关键是掌握平方差公式的实际运用,应明确两整数之和与两整数之积的奇偶性相同.

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目
18.2π是一个( )
| A. | 整数 | B. | 分数 | C. | 偶数 | D. | 无理数 |
17.比较$\sqrt{7}$-1与$\frac{\sqrt{7}}{2}$的大小,结果是( )
| A. | 后者大 | B. | 前者大 | C. | 一样大 | D. | 无法确定 |
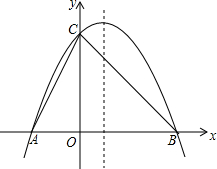 如图,已知抛物线y=ax2-2ax+4与x轴交于A、B两点,与y轴交于点C,且OB=OC.
如图,已知抛物线y=ax2-2ax+4与x轴交于A、B两点,与y轴交于点C,且OB=OC.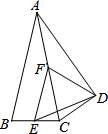 如图,△ABC中,AB=AC,以AC为斜边作Rt△ADC,使∠ADC=90°,∠CAD=∠CAB=26°,E、F分别是BC、AC的中点,则∠EDF等于51°.
如图,△ABC中,AB=AC,以AC为斜边作Rt△ADC,使∠ADC=90°,∠CAD=∠CAB=26°,E、F分别是BC、AC的中点,则∠EDF等于51°.