题目内容
6.探索图表的规律如图是2000年八月份的日历.(1)日历中的灰色方框中的9个数之和与该方框正中间的数有什么关系?
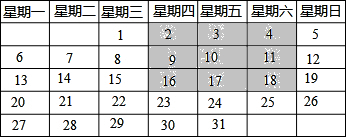
(2)这个关系对其它这样的方框成立吗?你能用代数式表示这个关系吗?
(3)这样框出的9个数之和能等于①107;②207;③270吗?若能,请求出最大数和最小数,若不能,请说明理由.
分析 (1)观察日历得到9个数的和为中间数的9倍;
(2)设中间的数为a,表示出其他8个数,求出之和即可;
(3)根据(2)中关系式列出方程,解方程后根据a是否为整数且a-8≥1、a+8≤31取舍即可,根据a-8=1取得最小值,a+8=31时取得最大值即可得.
解答 解:(1)∵日历中的灰色方框中的9个数之和为2+18+3+17+4+16+9+11+10=90,
∴9个数的和为中间数的9倍;
(2)任意框9个数,设中间的数为a,则左右两边数为a-1,a+1,上行邻数为(a-7),下行邻数为(a+7),
左右上角邻数为(a-8),(a-6),左右下角邻数为(a+6),(a+8),
之和为a+a-1+a+1+a-7+a+7+a-8+a-6+a+6+a+8=9a;
(3)若9个数之和能等于107,则9a=107,解得a=11$\frac{8}{9}$,
∵a不是整数,
∴9个数之和不能等于107;
若9个数之和能等于207,则9a=207,解得a=23,
∵a是整数,且a+8=31,
∴9个数之和能等于207;
若9个数之和能等于270,则9a=270,解得a=30,
∵a+8=38>31,
∴9个数之和不能等于270;
当a-8=1,即a=9时,取得最小值,最小值9a=81,
当a+8=31,即a=23时,取得最大值,最大值9a=207.
点评 本题考查了一元一次方程的应用,通过观察,分析、归纳并发现其中的规律,并应用发现的规律解决问题是学生应该具备的基本能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
1.定义一种新运算:观察下列式:
(1)请你想一想:a⊙b=4a+b;
(2)若a≠b,那么a⊙b≠b⊙a(填入“=”或“≠”);
(3)若a⊙(-2b)=4,请计算 (a-b)⊙(2a+b)的值.
| 1⊙3=1×4+3=7 | 3⊙(-1)=3×4-1=11 |
| 5⊙4=5×4+4=24 | 4⊙(-3)=4×4-3=13 |
(2)若a≠b,那么a⊙b≠b⊙a(填入“=”或“≠”);
(3)若a⊙(-2b)=4,请计算 (a-b)⊙(2a+b)的值.
 如图,在△ABC中,∠C=90°,AC=BC,点D在BC上,且∠BAD=15°.
如图,在△ABC中,∠C=90°,AC=BC,点D在BC上,且∠BAD=15°.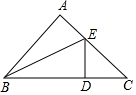 如图,△ABC中,AB=AC=1,∠BAC=90°,BE平分∠ABC交AC于E,ED⊥BC于D,求AE的长.
如图,△ABC中,AB=AC=1,∠BAC=90°,BE平分∠ABC交AC于E,ED⊥BC于D,求AE的长.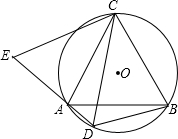 如图,△ABC内接于⊙O,AC=BC,D为弧AB上一点,延长DA至E,使CE=CD.
如图,△ABC内接于⊙O,AC=BC,D为弧AB上一点,延长DA至E,使CE=CD.