题目内容
12. 如图,在△ABC中,D为AB边上一点,DE∥BC交AC于点E,若$\frac{AD}{BD}=\frac{3}{4}$,DE=4,则BC的长为$\frac{28}{3}$.
如图,在△ABC中,D为AB边上一点,DE∥BC交AC于点E,若$\frac{AD}{BD}=\frac{3}{4}$,DE=4,则BC的长为$\frac{28}{3}$.
分析 根据相似三角形的判定和性质得到比例式,代入数据即可得到结论.
解答 解:∵$\frac{AD}{BD}=\frac{3}{4}$,
∴$\frac{AD}{AB}=\frac{3}{7}$,
∵DE∥BC,
∴△ADE∽△ABC,
∴$\frac{DE}{BC}=\frac{3}{7}$,
∵DE=4,
∴BC=$\frac{28}{3}$,
故答案为:$\frac{28}{3}$.
点评 本题考查了相似三角形的判定和性质,熟练掌握相似三角形的判定和性质是解题的关键.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
2.将两个斜边长相等的三角形纸片如图①放置,其中∠ACB=∠CED=90°,∠A=45°,∠D=30°.把△DCE绕点C顺时针旋转15°得到△D1CE1,如图②,连接D1B,则∠E1D1B的度数为( )
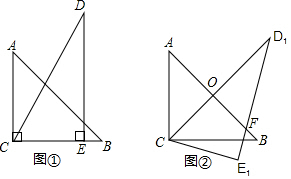

| A. | 10° | B. | 15° | C. | 7.5° | D. | 20° |
4.已知在△ABC中∠A=40°,∠B=50°,则△ABC为( )
| A. | 锐角三角形 | B. | 钝角三角形 | C. | 直角三角形 | D. | 以上都有可能 |
2.北京等5个城市的国际标准时间(单位:小时)可在数轴上表示如下:

如果将两地国际标准时间的差简称为时差,那么下列说法中正确的是( )

如果将两地国际标准时间的差简称为时差,那么下列说法中正确的是( )
| A. | 汉城与纽约的时差为13小时 | B. | 北京与纽约的时差为13小时 | ||
| C. | 北京与纽约的时差为14小时 | D. | 北京与多伦多的时差为14小时 |
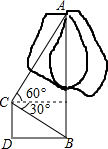 为改变哈尔滨市的交通状况,在大直街拓宽工程中,要伐掉一棵树AB,在地面上事先划定以B为圆心,半径与AB等长的圆形危险区,现在某工人站在离B点3米远的D处,从C点测得树的顶端A点的仰角为60°,树的底部B点的俯角为30°,那么距离B点7米远,才是安全区域.(结果保留整数,$\sqrt{3}$≈1.732)
为改变哈尔滨市的交通状况,在大直街拓宽工程中,要伐掉一棵树AB,在地面上事先划定以B为圆心,半径与AB等长的圆形危险区,现在某工人站在离B点3米远的D处,从C点测得树的顶端A点的仰角为60°,树的底部B点的俯角为30°,那么距离B点7米远,才是安全区域.(结果保留整数,$\sqrt{3}$≈1.732)