题目内容
11.已知x、y为正数,且|x2-4|与$\sqrt{{y}^{2}-3}$互为相反数,如果以x、y的长为直角边作直角三角形,那么以这个直角三角形的斜边为边长的正方形的面积为( )| A. | 5 | B. | 25 | C. | 7 | D. | 15 |
分析 本题可根据“两个非负数相加和为0,则这两个非负数的值均为0”解出x、y的值,然后运用勾股定理求出斜边的长.斜边长的平方即为正方形的面积.
解答 解:依题意得:x2-4=0,y2-3=0,
∴x=±2,y=±$\sqrt{3}$,
∵x、y为正数,
∴x=2,y=$\sqrt{3}$,
斜边长=$\sqrt{4+3}$=$\sqrt{7}$,
所以正方形的面积=($\sqrt{7}$)2=7.
故选C.
点评 本题考查了勾股定理与非负数,解这类题的关键是利用直角三角形,用勾股定理来寻求未知系数的等量关系.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
10.将分式$\frac{x+y}{{x}^{2}{+y}^{2}}$中x、y的值均变为原来的2倍,则分式的值( )
| A. | 缩小2倍 | B. | 扩大2倍 | C. | 不变 | D. | 不能确定 |
20.下列图形中,既是轴对称图形又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
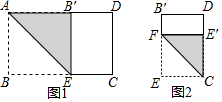 矩形纸片ABCD中,AD=10,AB=a(5<a<10)
矩形纸片ABCD中,AD=10,AB=a(5<a<10)