题目内容
5.如图,在平面直角坐标系中,点O为坐标原点,点C的坐标为(8,0),将线段OC向上平移a个单位长度得到线段AB(点B和点A分别是点C和点O的对应点),且a是方程$\frac{3a+5}{4}$-$\frac{a+3}{2}$=1的解,连接BC;(1)直接写出点B的坐标;B(8,5);
(2)动点P从点O出发,以每秒1个单位长度的速度沿折线O→A→B匀速运动,B为终点.设运动时间为t秒,线段AP的长为d,点P运动过程中请用含t的式子表示d;
(3)在(2)的条件下,在点P运动的同时,点Q以每秒2个单位长度的速度沿折线A→B→C→O匀速运动,连接OP和OQ,当OQ分四边形OABC的面积为1:3时,求出t的值及△OPQ的面积.
分析 (1)由$\frac{3a+5}{4}$-$\frac{a+3}{2}$=1得到a=5,可得点B坐标为(8,5).
(2)当0≤t<5时,d=5-t.当5≤t≤13时,d=t-5.
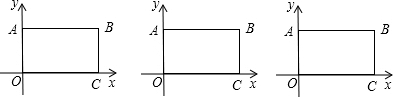
(3)分两种情形讨论①如图1中,当点Q是AB中点时,OQ分四边形OABC的面积为1:3.如图2中,当点Q是BC中点时,OQ分四边形OABC的面积为1:3,分别求解即可.
解答 解:(1)由$\frac{3a+5}{4}$-$\frac{a+3}{2}$=1得到a=5,
∴点B坐标为(8,5).
故答案为(8,5).
(2)当0≤t<5时,d=5-t.
当5≤t≤13时,d=t-5.
(3)①如图1中,当点Q是AB中点时,OQ分四边形OABC的面积为1:3,
此时t=$\frac{4}{2}$=2,OP=2,
∴S△POQ=$\frac{1}{2}$×2×4=4.
②如图2中,当点Q是BC中点时,OQ分四边形OABC的面积为1:3,
此时t=$\frac{12.5}{2}$=$\frac{25}{4}$s,AP=$\frac{25}{4}$-5=$\frac{5}{4}$,PB=8-$\frac{5}{4}$=$\frac{27}{4}$,
∴S△POQ=S矩形OABC-S△AOP-S△PQB-S△OCQ=5×8-$\frac{1}{2}$×5×$\frac{5}{4}$-$\frac{1}{2}$×8×$\frac{5}{2}$-$\frac{1}{2}$×$\frac{5}{2}$×$\frac{27}{4}$=$\frac{295}{16}$.
点评 本题考查三角形综合题、矩形的性质、三角形的面积、一元一次方程等知识,解题的关键是灵活运用所学知识解决问题,学会用分类讨论的思想思考问题,属于中考常考题型.

| A. | $2\sqrt{-8}=-2$ | B. | ${({-\sqrt{2}})^2}=4$ | C. | $\sqrt{{{({-3})}^2}}=-3$ | D. | $\sqrt{16}$=4 |
| A. | 角平分线 | B. | 高线 | C. | 中线 | D. | 中垂线 |
 如图,在Rt△ABC中,∠C=90°,AB=10,点D是直角边AC上一点,且满足cos∠ABD=$\frac{4}{5}$,∠A=∠CBD,求线段BD的长度.
如图,在Rt△ABC中,∠C=90°,AB=10,点D是直角边AC上一点,且满足cos∠ABD=$\frac{4}{5}$,∠A=∠CBD,求线段BD的长度.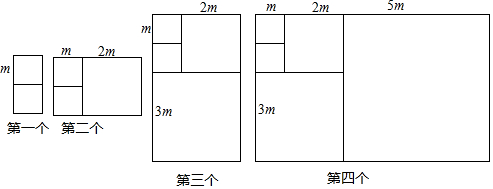
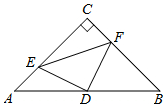 如图,在△ABC中,∠C=90°,AC=BC=4,D是AB的中点,点E、F分别在AC、BC边上运动(点E不与点A、C重合),且保持AE=CF,连接DE、DF、EF.在此运动变化的过程中,有下列结论:①△DFE是等腰直角三角形;②四边形CEDF不可能为正方形;③四边形CEDF的面积随点E位置的改变而发生变化;④点C、E、D、F四点在同一个圆上,且该圆的面积最小为4π.其中错误结论的个数是( )个.
如图,在△ABC中,∠C=90°,AC=BC=4,D是AB的中点,点E、F分别在AC、BC边上运动(点E不与点A、C重合),且保持AE=CF,连接DE、DF、EF.在此运动变化的过程中,有下列结论:①△DFE是等腰直角三角形;②四边形CEDF不可能为正方形;③四边形CEDF的面积随点E位置的改变而发生变化;④点C、E、D、F四点在同一个圆上,且该圆的面积最小为4π.其中错误结论的个数是( )个.