题目内容
14.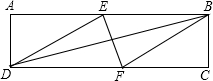 在矩形ABCD中有一个菱形BEDF(点E、F分别在线段AB、CD上)记它们的面积分别为S矩形ABCD和S菱形BEDF,若S矩形ABCD:S菱形BFDE=(2+$\sqrt{3}$):2,给出如下结论:①AB:BE=(2+$\sqrt{3}$):2;②AE=BE;③tan∠EDF=$\frac{\sqrt{3}}{3}$;④∠FBC=60°.其中正确的结论的序号是①③④(把所有正确结论的序号都填在横线上)
在矩形ABCD中有一个菱形BEDF(点E、F分别在线段AB、CD上)记它们的面积分别为S矩形ABCD和S菱形BEDF,若S矩形ABCD:S菱形BFDE=(2+$\sqrt{3}$):2,给出如下结论:①AB:BE=(2+$\sqrt{3}$):2;②AE=BE;③tan∠EDF=$\frac{\sqrt{3}}{3}$;④∠FBC=60°.其中正确的结论的序号是①③④(把所有正确结论的序号都填在横线上)
分析 由图可得矩形的宽和菱形的高相等,根据它们的面积关系即可得出AB:BE的值;根据AE:BE=(2+$\sqrt{3}$):2,可得AE=BE错误;由菱形的性质得出DE∥BF,DE=BE,得出∠BFC=∠EDF,由三角函数求出∠ADE=60°,得出∠ADC=∠C=90°,求出∠EDF=30°,即可得到tan∠EDF的值;根据∠BFC=30°,即可得出∠FBC=60°;最后得出正确的结论.
解答  解:如图所示,∵S矩形ABCD:S菱形BFDE=$\frac{AB•BC}{BE•BC}$=(2+$\sqrt{3}$):2,
解:如图所示,∵S矩形ABCD:S菱形BFDE=$\frac{AB•BC}{BE•BC}$=(2+$\sqrt{3}$):2,
∴AB:BE=(2+$\sqrt{3}$):2,
故①正确;
∵AB:BE=(2+$\sqrt{3}$):2,
∴AE:BE=$\sqrt{3}$:2,
故②错误;
∵四边形BFDE是菱形,
∴DE∥BF,DE=BE,
∴∠BFC=∠EDF,
∵sin∠ADE=$\frac{AE}{DE}$=$\frac{AE}{BE}$=$\frac{\sqrt{3}}{2}$,
∴∠ADE=60°,
∵∠ADC=∠C=90°,
∴∠EDF=90°-60°=30°,
∴tan∠EDF=$\frac{\sqrt{3}}{3}$,
故③正确;
∵DE∥BF,
∴∠BFC=30°,
∴∠FBC=90°-30°=60°,
故④正确;
综上所述,正确的结论为①③④.
故答案为:①③④.
点评 本题属于四边形综合题,主要考查了矩形的性质、菱形的性质、三角函数等知识的综合应用,熟练掌握矩形和菱形的性质,由矩形和菱形的性质得出AB:BE的值是解决问题的关键.

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目
4.若|2016-a|+$\sqrt{a-2017}$=a,则a-20162的值是( )
| A. | 2014 | B. | 2015 | C. | 2016 | D. | 2017 |
5.一元二次方程x2+2x+2=0的根的情况是( )
| A. | 有两个不相等的实数根 | B. | 有两个相等的实数根 | ||
| C. | 没有实数根 | D. | 只有一个实数根 |
9.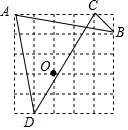 如图为5×5的网格图,A,B,C,D,O均在格点上,则点O是( )
如图为5×5的网格图,A,B,C,D,O均在格点上,则点O是( )
 如图为5×5的网格图,A,B,C,D,O均在格点上,则点O是( )
如图为5×5的网格图,A,B,C,D,O均在格点上,则点O是( )| A. | △ACD的外心 | B. | △ABC的外心 | C. | △ACD的内心 | D. | △ABC的内心 |
19.H7N9时一种新型禽流感,其病毒颗粒呈多形性,其中球形病毒的最大直径为0.00000012米,这一直径用科学记数法表示为( )
| A. | 1.2×10-7米 | B. | 1.2×10-8米 | C. | 12×10-8米 | D. | 12×10-9米 |
3.数字3300用科学记数法表示为( )
| A. | 0.33×104 | B. | 3.3×103 | C. | 3.3×104 | D. | 33×103 |
 如图,矩形ABCD中,BC=2,将矩形ABCD绕点D顺时针旋转90°,点A,C分别落在点A′、C′处,并且点A′,C′,B在同一条直线上,则tan∠ABA′的值为$\frac{\sqrt{5}-1}{2}$.
如图,矩形ABCD中,BC=2,将矩形ABCD绕点D顺时针旋转90°,点A,C分别落在点A′、C′处,并且点A′,C′,B在同一条直线上,则tan∠ABA′的值为$\frac{\sqrt{5}-1}{2}$. 如图,将矩形纸片ABCD沿EF折叠,使点C与点A重合,连接CE,若AB=2,BC=3,则CE的长为$\frac{13}{6}$.
如图,将矩形纸片ABCD沿EF折叠,使点C与点A重合,连接CE,若AB=2,BC=3,则CE的长为$\frac{13}{6}$. 如图,O对应的有序数对为(1,3)有一个英文单词的字母顺序对应如图中的有序数对分别为(1,2),(5,1),(5,2),(5,2),(1,3),请你把这个英文单词写出来或者翻译成中文为HELLO.
如图,O对应的有序数对为(1,3)有一个英文单词的字母顺序对应如图中的有序数对分别为(1,2),(5,1),(5,2),(5,2),(1,3),请你把这个英文单词写出来或者翻译成中文为HELLO.