题目内容
13.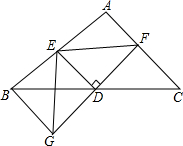 如图,△ABC中,D是BC的中点,过D点的直线GF交AC于点F,交AC的平行线BG于点G,DE⊥GF交AB于点E,连接EG.
如图,△ABC中,D是BC的中点,过D点的直线GF交AC于点F,交AC的平行线BG于点G,DE⊥GF交AB于点E,连接EG.(1)求证:BG=CF;
(2)若∠BAC=90°,请你判断BE,CF与EF三条线段的数量关系,并证明.
分析 (1)由BG∥AC得出∠DBG=∠DCF,从而根据ASA证得△BGD≌△CFD,即可证得结论.
(2)根据△BGD≌△CFD得出GD=FD,BG=CF,然后根据线段的垂直平分线的性质求得EG=EF,根据平行线的性质证得∠EBG=90°,最后根据勾股定理即可求得BE2+BG2=EG2,通过等量代换即可得到BE、CF、EF之间存在的等量关系.
解答 解:(1)∵BG∥AC,
∴∠DBG=∠DCF,
∵D是BC的中点,
∴BD=CD,
在△BGD和△CFD中,
$\left\{\begin{array}{l}{∠DBG=∠DCF}\\{BD=CD}\\{∠BDG=∠CDF}\end{array}\right.$,
∴△BGD≌△CFD(ASA),
∴BG=CF.
(2)BE2+CF2=EF2;
理由:∵△BGD≌△CFD,
∴GD=FD,BG=CF,
又∵DE⊥FG,
∴EG=EF(垂直平分线上的点到线段两端点的距离相等),
∵∠A=90°,AC∥BG,
∴∠EBG=90°,
∴在△EBG中,BE2+BG2=EG2,
即BE2+CF2=EF2.
点评 本题考查了平行线的性质,三角形全等的判定和性质,线段的垂直平分线的性质以及勾股定理的应用,熟练掌握性质定理是解题的关键.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
2.LED照明灯是利用第四代绿色光源LED做成的一种照明灯具,该灯具具有节能、环保、寿命长、体积小等特点,其耗电量仅为相同光通量白炽灯的20%,某商场计划购进甲、乙两种型号的LED照明灯共1200只,这两种照明灯的进价,售价如下表所示.
(1)求出该商场怎样进货,才能使总进价恰好为34000元;
(2)求出该商场怎样进货,才能使该商场售完这批LED照明灯的利润恰好为这批LED照明灯的总进价的45%,并求此时的利润(利润用科学记数法表示)
| 甲型号LED照明灯 | 乙型号LED照明灯 | |
| 进价(元/只) | 20 | 40 |
| 售价(元/只) | 30 | 55 |
(2)求出该商场怎样进货,才能使该商场售完这批LED照明灯的利润恰好为这批LED照明灯的总进价的45%,并求此时的利润(利润用科学记数法表示)
 如图,在地面上离旗杆BC底部18米的A处,用测角仪测得旗杆顶端C的仰角为30°,已知测角仪AD的高度为1.5米,那么旗杆BC的高度为6$\sqrt{3}$+1.5米.
如图,在地面上离旗杆BC底部18米的A处,用测角仪测得旗杆顶端C的仰角为30°,已知测角仪AD的高度为1.5米,那么旗杆BC的高度为6$\sqrt{3}$+1.5米.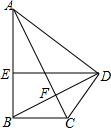 如图,在四边形ABCD中,AB=8,AC=4$\sqrt{5}$,∠ABC=90°,AB=AD,BC=CD,过点D作DE∥BC,交AB于点E,连接AC,BD,AC与BD交于点F.
如图,在四边形ABCD中,AB=8,AC=4$\sqrt{5}$,∠ABC=90°,AB=AD,BC=CD,过点D作DE∥BC,交AB于点E,连接AC,BD,AC与BD交于点F.
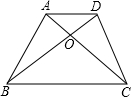 如图,梯形ABCD中,AD∥BC,AC交BD于O,△AOD与△BOC的面积分别是4和9平方单位,则梯形ABCD的面积是25.
如图,梯形ABCD中,AD∥BC,AC交BD于O,△AOD与△BOC的面积分别是4和9平方单位,则梯形ABCD的面积是25.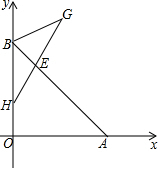 如图,点B(0,b),点A(a,0)分别在y轴、x轴正半轴上,且满足
如图,点B(0,b),点A(a,0)分别在y轴、x轴正半轴上,且满足