题目内容
18．
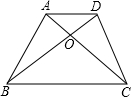如图，梯形ABCD中，AD∥BC，AC交BD于O，△AOD与△BOC的面积分别是4和9平方单位，则梯形ABCD的面积是25．
分析 先由平行线证明△AOD∽△COB，利用面积求出相似三角形对应边的比，再利用等高不同底求出另外两个三角形的面积，四个三角形的面积之和就是梯形面积．
解答 解：∵AD∥BC，
∴△AOD∽△COB，
∵S△AOD=4，S△BOC=9，
∴OD：OB=2：3，
∵△AOD，△AOB是同高不同底的三角形，
∴S△AOD：S△AOB=2：3，
∵S△AOD=4，
∴S△AOB=6，
同理可求S△COD=6，
∴S梯形ABCD=4+9+6+6=25，
故答案为：25．
点评 本题考查了梯形、三角形的面积、相似三角形的判定和性质．解题的关键是利用三角形相似，由面积之比求出边之比，然后再利用同高不等底的三角形的面积比等于它们的底之比，求出另外两个三角形的面积，最后求出梯形的面积．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
6．若x-1=2（y+1）=3（z+2），则x2+y2+z2可取得的最小值为（ ）
| A． | 6 | B． | $\frac{41}{7}$ | C． | $\frac{83}{14}$ | D． | $\frac{293}{49}$ |
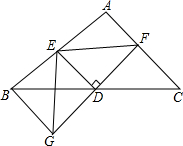如图，△ABC中，D是BC的中点，过D点的直线GF交AC于点F，交AC的平行线BG于点G，DE⊥GF交AB于点E，连接EG．