题目内容
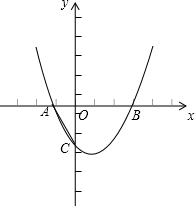 如图,二次函数y=ax2+bx-2的图象与x轴的两个交点分别为A(-1,0),B(2,0),与y轴的交点为C,
如图,二次函数y=ax2+bx-2的图象与x轴的两个交点分别为A(-1,0),B(2,0),与y轴的交点为C,(1)求二次函数的解析式;
(2)若点P的坐标为(
| 3 |
| 2 |
(3)若M是在y轴右侧的二次函数图象上的一点,过点M作直线AC的垂线,垂足为H,当△CHM∽△AOC(点C与点A对应,点H与点O对应,点M与点C对应)时,求点M的坐标.
考点:二次函数综合题
专题:
分析:(1)把点A、B的坐标代入二次函数y=ax2+bx-2的解析式求出a、b的值,即可得到二次函数解析式;
(2)由抛物线的解析式为y=x2-x-2,求得C(0,-2),根据A、P的坐标即可求得PA、PC的长,从而证明PA=PC.
(3)根据相似三角形对应角相等可得∠MCH=∠CAO.
(i)当点H在点C上方时,根据(2)的结论,点M为直线PC与抛物线的另一交点,求出直线PC的解析式,与抛物线的解析式联立求解即可得到点M的坐标;
(ii)当点H在点C下方时,利用同位角相等,两直线平行判定CM∥x轴,从而得到点M的纵坐标与点C的纵坐标相同,是-2,代入抛物线解析式计算即可.
(2)由抛物线的解析式为y=x2-x-2,求得C(0,-2),根据A、P的坐标即可求得PA、PC的长,从而证明PA=PC.
(3)根据相似三角形对应角相等可得∠MCH=∠CAO.
(i)当点H在点C上方时,根据(2)的结论,点M为直线PC与抛物线的另一交点,求出直线PC的解析式,与抛物线的解析式联立求解即可得到点M的坐标;
(ii)当点H在点C下方时,利用同位角相等,两直线平行判定CM∥x轴,从而得到点M的纵坐标与点C的纵坐标相同,是-2,代入抛物线解析式计算即可.
解答:解:(1)∵二次函数y=ax2+bx-2图象交x轴于A(-1,0),B(2,0),
∴
解得
.
∴抛物线的解析式为y=x2-x-2;
(2)由抛物线的解析式为y=x2-x-2,则C(0,-2).
∵P的坐标为(
,0),A(-1,0),
∴PA=
+1=
,PC=
=
,
∴PA=PC;
(3)∵△CHM∽△AOC,
∴∠MCH=∠CAO.
(i)如图2,当点H在点C上方时.
由(2)知,PA=PC,
∴∠PCA=∠CAP,即∠PCA=∠CAO.
又∵∠MCH=∠CAO,即∠MCA=∠CAO,
∴∠PCA=∠MCH,
∴点M是线段CP的延长线与抛物线的交点.
设直线CM的解析式为y=kx-2(k≠0),
把P(
,0)代入,得
k-2=0,
解得,k=
,则直线CM的解析式是y=
x-2,
∴
,
解得,
(舍去),或
,
 ∴M(
∴M(
,
);
(ii)如图3,点H在点C下方时.
∵∠MCH=∠CAO,
∴CM∥x轴,
∴yM=-2,
∴x2-x-2=-2,
解得x1=0(舍去),x2=1
∴M(1,-2).
综上所述,点M的坐标是M(
,
)或M(1,-2).
∴
|
解得
|
∴抛物线的解析式为y=x2-x-2;
(2)由抛物线的解析式为y=x2-x-2,则C(0,-2).
∵P的坐标为(
| 3 |
| 2 |
∴PA=
| 3 |
| 2 |
| 5 |
| 2 |
(
|
| 5 |
| 2 |
∴PA=PC;
(3)∵△CHM∽△AOC,

∴∠MCH=∠CAO.
(i)如图2,当点H在点C上方时.
由(2)知,PA=PC,
∴∠PCA=∠CAP,即∠PCA=∠CAO.
又∵∠MCH=∠CAO,即∠MCA=∠CAO,
∴∠PCA=∠MCH,
∴点M是线段CP的延长线与抛物线的交点.
设直线CM的解析式为y=kx-2(k≠0),
把P(
| 3 |
| 2 |
| 3 |
| 2 |
解得,k=
| 4 |
| 3 |
| 4 |
| 3 |
∴
|
解得,
|
|
 ∴M(
∴M(| 7 |
| 3 |
| 10 |
| 9 |
(ii)如图3,点H在点C下方时.
∵∠MCH=∠CAO,
∴CM∥x轴,
∴yM=-2,
∴x2-x-2=-2,
解得x1=0(舍去),x2=1
∴M(1,-2).
综上所述,点M的坐标是M(
| 7 |
| 3 |
| 10 |
| 9 |
点评:本题是对二次函数的综合考查,主要利用了待定系数法求二次函数解析式,勾股定理,相似三角形的性质,两函数图象交点的求解方法,综合性较强,难度较大,要注意分情况讨论求解.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
解方程-3x+5=2x-1时,移项正确的是( )
| A、3x-2x=-1+5 |
| B、-3x-2x=5-1 |
| C、3x-2x=-1-5 |
| D、-3x-2x=-1-5 |
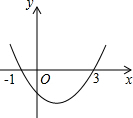 已知二次函数y=ax2+bx+c的图象如图所示,它与x轴的两个交点分别为(-1,0),(3,0),对于下列命题:①b+2a=0②abc<0③a-2b+4c<0④8a+c>0,其中正确的有( )
已知二次函数y=ax2+bx+c的图象如图所示,它与x轴的两个交点分别为(-1,0),(3,0),对于下列命题:①b+2a=0②abc<0③a-2b+4c<0④8a+c>0,其中正确的有( )| A、3个 | B、2个 | C、1个 | D、0个 |
以下列各组线段为边作三角形,不能构成直角三角形的是( )
A、1,
| ||||||
B、
| ||||||
| C、5,12,13 | ||||||
| D、9,40,41 |
若x2+kx+16能通过因式分解写成(a+b)2的形式,则k的值是( )
| A、8 | B、-8 | C、±8 | D、±4 |