题目内容
如图,在直角△BAD中,延长斜边BD到点C,使DC=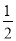 BD,连接AC,若tanB=
BD,连接AC,若tanB=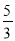 ,则tan∠CAD的值( )
,则tan∠CAD的值( )
A. 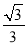 B.
B. 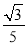 C.
C. 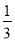 D.
D. 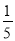
 D
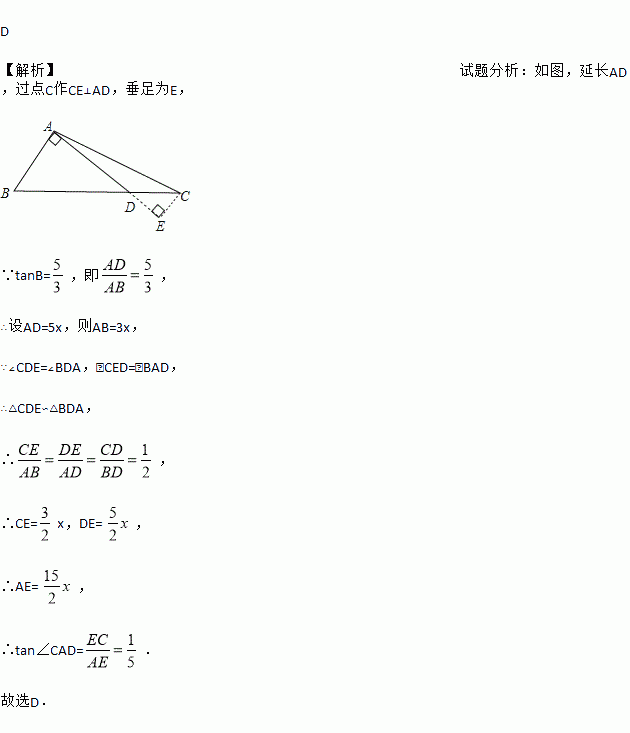
【解析】试题分析:如图,延长AD,过点C作CE⊥AD,垂足为E,
∵tanB=,即,
∴设AD=5x,则AB=3x,
∵∠CDE=∠BDA,∠CED=∠BAD,
∴△CDE∽△BDA,
∴,
∴CE=x,DE= ,
∴AE= ,
∴tan∠CAD=.
故选D.
D
【解析】试题分析:如图,延长AD,过点C作CE⊥AD,垂足为E,
∵tanB=,即,
∴设AD=5x,则AB=3x,
∵∠CDE=∠BDA,∠CED=∠BAD,
∴△CDE∽△BDA,
∴,
∴CE=x,DE= ,
∴AE= ,
∴tan∠CAD=.
故选D.
 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案在Rt△ABC中,∠C=90°,∠A、∠B、∠C所对的边分别为a、b、c,下列等式中不一定成立的是( )
A. b=atanB B. a=ccosB C. c=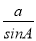 D. a=bcosA
D. a=bcosA
 D
【解析】∵∠C=90°,∠A、∠B、∠C所对的边分别为a、b、c,
∴A.tanB= ,则b=atanB,故本选项正确,
B.cosB= ,故本选项正确,
C.sinA= ,故本选项正确,
D.cosA= ,故本选项错误,
故选D.
D
【解析】∵∠C=90°,∠A、∠B、∠C所对的边分别为a、b、c,
∴A.tanB= ,则b=atanB,故本选项正确,
B.cosB= ,故本选项正确,
C.sinA= ,故本选项正确,
D.cosA= ,故本选项错误,
故选D. 在△ABC中,∠C-90°,若tanB=2,a=1,则b=________.
 2
【解析】试题解析:在Rt△ABC中,
∵∠C=90°,
∴AB为斜边.
∴b=AC•tanB
=a•tanB
=2.
故答案为:2.
2
【解析】试题解析:在Rt△ABC中,
∵∠C=90°,
∴AB为斜边.
∴b=AC•tanB
=a•tanB
=2.
故答案为:2. 如图所示为农村居民住宅侧面截面图,屋坡AF、AG分别架在墙体的点B,点C处,且AB=AC,侧面四边形BDEC为长方形.若测得∠FAG=110°,则∠FBD=( )
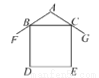
A. 35° B. 40° C. 55° D. 70°
 C
【解析】在△ABC中,AB=AC,∠BAC=110°,根据等腰三角形的性质和三角形的内角和定理可得∠ABC=35°,由四边形BDEC为长方形可得∠DBC=90°,再由平角的定义可得∠FBD=180°-∠ABC-∠DBC=180°-35°-90°=55°,故选C.
C
【解析】在△ABC中,AB=AC,∠BAC=110°,根据等腰三角形的性质和三角形的内角和定理可得∠ABC=35°,由四边形BDEC为长方形可得∠DBC=90°,再由平角的定义可得∠FBD=180°-∠ABC-∠DBC=180°-35°-90°=55°,故选C. 如图,矩形ABCD是供一机动车停放的车位示意图,已知BC=2m,CD=5.4m,∠DCF=30°.请你计算车位所占的宽度EF约为多少米?(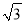 ≈1.73,结果保留一位小数)
≈1.73,结果保留一位小数)
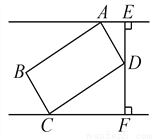
 4.4米
【解析】试题分析:分别在Rt△BCF和Rt△AEF中求得DF和DE的长后,相加即可得到EF的长.
试题解析:
在Rt△DCF中,
∵CD=5.4m,∠DCF=30°,
∴sin∠DCF=,
∴DF=2.7m,
∵∠CDF+∠DCF=90°∠ADE+∠CDF=90°,
∴∠ADE=∠DCF=30°,
∵AD=BC=2,
∴cos∠...
4.4米
【解析】试题分析:分别在Rt△BCF和Rt△AEF中求得DF和DE的长后,相加即可得到EF的长.
试题解析:
在Rt△DCF中,
∵CD=5.4m,∠DCF=30°,
∴sin∠DCF=,
∴DF=2.7m,
∵∠CDF+∠DCF=90°∠ADE+∠CDF=90°,
∴∠ADE=∠DCF=30°,
∵AD=BC=2,
∴cos∠... 国家规定,中小学生每天在校体育活动时间不低于1小时,为了解这项政策的落实情况,有关部门就“你某天在校体育活动时间是多少”的问题,在某校随机抽查了部分学生,再根据活动时间t(小时)进行分组(A组:t<0.5,B组:0.5≤t<1,C组:1≤t<1.5,D组:t≥1.5),绘制成如下两幅不完整统计图,请根据图中信息回答问题:
(1)此次抽查的学生数为 人;
(2)补全条形统计图;
(3)从抽查的学生中随机询问一名学生,该生当天在校体育活动时间低于1小时的概率是 ;
(4)若当天在校学生数为1200人,请估计在当天达到国家规定体育活动时间的学生有 人.

 (1)300;(2)补图见解析;(3)40%;(4)720人.
【解析】试题分析:(1)根据题意即可得到结论;
(2)求出C组的人数,A组的人数补全条形统计图即可;
(3)根据概率公式即可得到结论;
(4)用总人数乘以达到国家规定体育活动时间的百分比即可得到结论.
试题解析:(1)60÷20%=300(人),
答:此次抽查的学生数为300人.
故答案为:3...
(1)300;(2)补图见解析;(3)40%;(4)720人.
【解析】试题分析:(1)根据题意即可得到结论;
(2)求出C组的人数,A组的人数补全条形统计图即可;
(3)根据概率公式即可得到结论;
(4)用总人数乘以达到国家规定体育活动时间的百分比即可得到结论.
试题解析:(1)60÷20%=300(人),
答:此次抽查的学生数为300人.
故答案为:3... 下列说法中,正确的是( )
A. 不可能事件发生的概率为0
B. 随机事件发生的概率为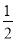
C. 概率很小的事件不可能发生
D. 投掷一枚质地均匀的硬币100次,正面朝上的次数一定为50次
 A
【解析】试题分析:不可能事件发生的概率为0,故A正确;
随机事件发生的概率为在0到1之间,故B错误;
概率很小的事件也可能发生,故C错误;
投掷一枚质地均匀的硬币100次,正面向上的次数为50次是随机事件,D错误;
故选A.
A
【解析】试题分析:不可能事件发生的概率为0,故A正确;
随机事件发生的概率为在0到1之间,故B错误;
概率很小的事件也可能发生,故C错误;
投掷一枚质地均匀的硬币100次,正面向上的次数为50次是随机事件,D错误;
故选A. 小球在如图所示的地板上自由滚动,并随机地停留在某块方砖上,每一块方砖除颜色外完全相同,它最终停留在黑色方砖上的概率是 .

 .
【解析】
试题分析:根据几何概率的求法:最终停留在黑色的方砖上的概率就是黑色区域的面积与总面积的比值.观察这个图可知:黑色区域(4块)的面积占总面积(9块)的,则它最终停留在黑色方砖上的概率是.
故答案为:.
.
【解析】
试题分析:根据几何概率的求法:最终停留在黑色的方砖上的概率就是黑色区域的面积与总面积的比值.观察这个图可知:黑色区域(4块)的面积占总面积(9块)的,则它最终停留在黑色方砖上的概率是.
故答案为:. 求不等式1+x>x-1成立的x取值范围.
 x可取一切实数
【解析】
试题分析:根据不等式的基本性质求出不等式1+x>x-1的解集即可判断.
不等式1+x>x-1两边同时减去x得1>-1,恒成立
则不等式1+x>x-1成立的x取值范围是x可取一切实数.
x可取一切实数
【解析】
试题分析:根据不等式的基本性质求出不等式1+x>x-1的解集即可判断.
不等式1+x>x-1两边同时减去x得1>-1,恒成立
则不等式1+x>x-1成立的x取值范围是x可取一切实数.