题目内容
20.(1)解不等式组$\left\{\begin{array}{l}x+2≥1\\ 2(x+3)-3>3x\end{array}\right.$(2)解方程:x2+3x-2=0.
分析 (1)分别求出两个不等式的解集,求其公共解.
(2)首先确定a,b,c的值,然后检验方程是否有解,若有解,代入公式即可求解.
解答 解:(1)$\left\{\begin{array}{l}{x+2≥1①}\\{2(x+3)-3>3x②}\end{array}\right.$
由①得x≥-1,
由②得x<3,
∴不等式组的解集为-1≤x<3.
(2)x2+3x-2=0.
a=1,b=3,c=-2,
△=32-4×1×(-2)=17
∴$x=\frac{{-3±\sqrt{17}}}{2}$,
∴${x_1}=\frac{{-3+\sqrt{17}}}{2}$,${x_2}=\frac{{-3-\sqrt{17}}}{2}$.
点评 本题考查了解一元二次方程的方法-公式法,解不等式组,求不等式的公共解,要遵循以下原则:同大取较大,同小取较小,小大大小中间找,大大小小解不了.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
11.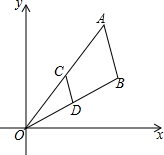 如图,线段AB两个端点的坐标分别为A(6,8),B(7,4),以原点为位似中心,在第一象限内将线段AB缩小为原来的$\frac{1}{2}$后得到线段CD.则端点C的坐标为( )
如图,线段AB两个端点的坐标分别为A(6,8),B(7,4),以原点为位似中心,在第一象限内将线段AB缩小为原来的$\frac{1}{2}$后得到线段CD.则端点C的坐标为( )
 如图,线段AB两个端点的坐标分别为A(6,8),B(7,4),以原点为位似中心,在第一象限内将线段AB缩小为原来的$\frac{1}{2}$后得到线段CD.则端点C的坐标为( )
如图,线段AB两个端点的坐标分别为A(6,8),B(7,4),以原点为位似中心,在第一象限内将线段AB缩小为原来的$\frac{1}{2}$后得到线段CD.则端点C的坐标为( )| A. | (3,3) | B. | (4,3) | C. | (3,4) | D. | ($\frac{7}{2}$,2) |
8.已知反比例函数$y=-\frac{2}{x}$,当x<0时,它的图象在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
5.下列运算正确的是( )
| A. | (-2x2)3=-6x6 | B. | (y+x)(-y+x)=y2-x2 | C. | (a3)2•a4=a9 | D. | 3$\sqrt{a}$+4$\sqrt{a}$=7$\sqrt{a}$ |
12.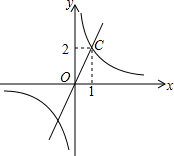 反比例函数y﹦$\frac{k}{x}$和正比例函数y﹦mx的图象如图所示.由此可以得到方程$\frac{k}{x}$﹦mx的实数根为( )
反比例函数y﹦$\frac{k}{x}$和正比例函数y﹦mx的图象如图所示.由此可以得到方程$\frac{k}{x}$﹦mx的实数根为( )
 反比例函数y﹦$\frac{k}{x}$和正比例函数y﹦mx的图象如图所示.由此可以得到方程$\frac{k}{x}$﹦mx的实数根为( )
反比例函数y﹦$\frac{k}{x}$和正比例函数y﹦mx的图象如图所示.由此可以得到方程$\frac{k}{x}$﹦mx的实数根为( )| A. | x=1 | B. | x=2 | C. | x1=1,x2=-1 | D. | x1=1,x2=-2 |
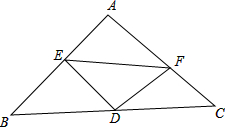 如图,Rt△ABC中,∠A=90°,AB=AC=2,点D是BC边的中点,点E是AB边上的一个动点(不与A、B重合),DF⊥DE交AC于F.设BE=x,FC=y.
如图,Rt△ABC中,∠A=90°,AB=AC=2,点D是BC边的中点,点E是AB边上的一个动点(不与A、B重合),DF⊥DE交AC于F.设BE=x,FC=y.