题目内容
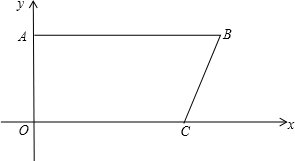
9.如图,在平面直角坐标系中,AB∥OC,A(0,12),B(a,c),C(b,0),并且a,b满足b=$\sqrt{a-21}$+$\sqrt{21-a}$+16.一动点P从点A出发,在线段AB上以每秒2个单位长度的速度向点B运动;动点Q从点O出发在线段OC上以每秒1个单位长度的速度向点C运动,点P、Q分别从点A、O同时出发,当点P运动到点B时,点Q随之停止运动.设运动时间为t(秒)(1)求B、C两点的坐标;
(2)当t为何值时,四边形PQCB是平行四边形?并求出此时P、Q两点的坐标;
(3)当t为何值时,△PQC是以PQ为腰的等腰三角形?并求出P、Q两点的坐标.
分析 (1)根据二次根式的性质得出a,b的值进而得出答案;
(2)由题意得:QP=2t,QO=t,PB=21-2t,QC=16-t,根据平行四边形的判定可得21-2t=16-t,再解方程即可;
(3)①当PQ=CQ时,122+t2=(16-t)2,解方程得到t的值,再求P点坐标;②当PQ=PC时,由题意得:QM=t,CM=16-2t,进而得到方程t=16-2t,再解方程即可.
解答 解:(1)∵b=$\sqrt{a-21}$+$\sqrt{21-a}$+16,
∴a=21,b=16,
故B(21,12)C(16,0);
(2)由题意得:AP=2t,QO=t,
则:PB=21-2t,QC=16-t,
∵当PB=QC时,四边形PQCB是平行四边形,
∴21-2t=16-t,
解得:t=5,
∴P(10,12)Q(5,0);
(3)当PQ=CQ时,过Q作QN⊥AB,
由题意得:122+t2=(16-t)2,
解得:t=$\frac{7}{2}$,
故P(7,12),Q($\frac{7}{2}$,0),
当PQ=PC时,过P作PM⊥x轴,
由题意得:QM=t,CM=16-2t,
则t=16-2t,
解得:t=$\frac{16}{3}$,2t=$\frac{32}{3}$,
故P( $\frac{32}{3}$,12),Q($\frac{16}{3}$,0).
点评 此题主要考查了平行四边形的判定,等腰三角形的判定,关键是注意分类讨论,不要漏解.

练习册系列答案
相关题目
17.为了参加市中学生篮球赛,某校一支篮球队购买了10双运动鞋,尺码如下表:
则这10双运动鞋尺码的众数和中位数分别为( )
| 尺码(cm) | 25 | 25.5 | 26 | 26.5 | 27 |
| 购买量(双) | 1 | 2 | 3 | 2 | 2 |
| A. | 25.5cm,26cm | B. | 26cm,25.5cm | C. | 25.5cm,25.5cm | D. | 26cm,26cm |
4. 如图所示,正四棱锥的俯视图为( )
如图所示,正四棱锥的俯视图为( )
 如图所示,正四棱锥的俯视图为( )
如图所示,正四棱锥的俯视图为( )| A. |  | B. |  | C. |  | D. |  |
1.算式(2+1)•(22+1)•(24+1)…(232+1)+1计算结果的个位数字是( )
| A. | 4 | B. | 6 | C. | 2 | D. | 8 |
18.在算式(-$\sqrt{0.3}$)□(-$\sqrt{0.3}$)□中填上运算符号,使结果最大,这个运算符号是( )
| A. | 加号 | B. | 减号 | C. | 乘号 | D. | 除号 |
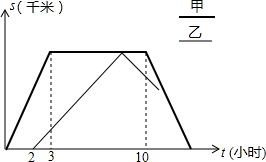 甲乙两车从姜堰去往扬州市,甲比乙早出发了2个小时,甲到达扬州市后停留一段时间返回,乙到达扬州市后立即返回.甲车往返的速度都为80千米/时,乙车往返的速度都为40千米/时,下图是两车距姜堰的路程S(千米)与行驶时间t(小时)之间的函数图象.请结合图象回答下列问题:
甲乙两车从姜堰去往扬州市,甲比乙早出发了2个小时,甲到达扬州市后停留一段时间返回,乙到达扬州市后立即返回.甲车往返的速度都为80千米/时,乙车往返的速度都为40千米/时,下图是两车距姜堰的路程S(千米)与行驶时间t(小时)之间的函数图象.请结合图象回答下列问题: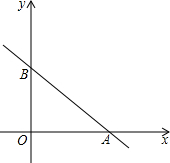 在平面直角坐标系中,一次函数的图象与坐标轴围成的三角形,叫做此一次函数的坐标三角形.例如,图中的一次函数的图象与x,y轴分别交于点A,B,则△OAB为此函数的坐标三角形.求函数y=-$\frac{3}{4}$x+3的坐标三角形的三条边长.
在平面直角坐标系中,一次函数的图象与坐标轴围成的三角形,叫做此一次函数的坐标三角形.例如,图中的一次函数的图象与x,y轴分别交于点A,B,则△OAB为此函数的坐标三角形.求函数y=-$\frac{3}{4}$x+3的坐标三角形的三条边长.