题目内容
10．x取何值时，代数式2x-5的值不小于代数式$\frac{1}{2}$（2-x）的值？分析 先根据题意得出关于x的不等式，再去分母，再去括号，再移项、再合并同类项即可．
解答 解：∵代数式2x-5的值不小于代数式$\frac{1}{2}$（2-x）的值，
∴2x-5≥$\frac{1}{2}$（2-x），解得x＞$\frac{12}{5}$．
点评 本题考查的是解一元一次不等式，熟知解一元一次不等式的基本步骤是解答此题的关键．
练习册系列答案
相关题目
1．算式（2+1）•（22+1）•（24+1）…（232+1）+1计算结果的个位数字是（ ）
| A． | 4 | B． | 6 | C． | 2 | D． | 8 |
18．在算式（-$\sqrt{0.3}$）□（-$\sqrt{0.3}$）□中填上运算符号，使结果最大，这个运算符号是（ ）
| A． | 加号 | B． | 减号 | C． | 乘号 | D． | 除号 |
5．
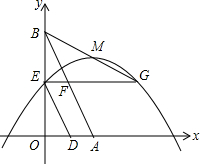已知：如图，直线y=-$\sqrt{3}$x+$\sqrt{3}$与x轴、y轴分别交于A、B两点，两动点D、E分别以1个单位长度/秒和$\sqrt{3}$个单位长度/秒的速度从A、B两点同时出发向O点运动（运动到O点停止）；过E点作EG∥OA交抛物线y=a（x-1）2+h（a＜0）于E、G两点，交AB于点F，连结DE、BG．若抛物线的顶点M恰好在BG上且四边形ADEF是菱形，则a、h的值分别为（ ）
已知：如图，直线y=-$\sqrt{3}$x+$\sqrt{3}$与x轴、y轴分别交于A、B两点，两动点D、E分别以1个单位长度/秒和$\sqrt{3}$个单位长度/秒的速度从A、B两点同时出发向O点运动（运动到O点停止）；过E点作EG∥OA交抛物线y=a（x-1）2+h（a＜0）于E、G两点，交AB于点F，连结DE、BG．若抛物线的顶点M恰好在BG上且四边形ADEF是菱形，则a、h的值分别为（ ）| A． | -$\frac{\sqrt{3}}{3}$、$\frac{2\sqrt{3}}{3}$ | B． | -$\frac{\sqrt{3}}{3}$、$\frac{3\sqrt{3}}{4}$ | C． | -$\frac{\sqrt{3}}{4}$、$\frac{3\sqrt{3}}{4}$ | D． | -$\frac{\sqrt{3}}{4}$、$\frac{2\sqrt{3}}{3}$ |
如图，点C是线段AB的中点，点D是线段AC上的一点，且DC=2AD，若DC=16cm，求线段DB的长度．
如图，O为直线AB上的一点，且∠AOC=$\frac{1}{2}$∠BOC，则∠BOC的度数是120°．