题目内容
8.方程2$\sqrt{1+x}$-$\sqrt{2+2\sqrt{1-{x}^{2}}}$=1的解是x=$\frac{\sqrt{3}}{2}$或x=-$\frac{\sqrt{3}}{2}$.分析 由二次根式有意义条件得出x的范围,利用完全平方根式化简原方程可得$\sqrt{1+x}$-$\sqrt{1-x}$=1,两次两边平方将无理方程化为整式方程,解之可得.
解答 解:∵$\left\{\begin{array}{l}{1+x≥0}\\{1-{x}^{2}≥0}\end{array}\right.$,
∴-1≤x≤1,
原方程可化为:2$\sqrt{1+x}$-$\sqrt{(\sqrt{1+x}+\sqrt{1-x})^{2}}$=1,
2$\sqrt{1+x}$-($\sqrt{1+x}$+$\sqrt{1-x}$)=1,
$\sqrt{1+x}$-$\sqrt{1-x}$=1,
两边平方可得:2-2$\sqrt{1-{x}^{2}}$=1,
∴$\sqrt{1-{x}^{2}}$=$\frac{1}{2}$,
∴1-x2=$\frac{1}{4}$,
解得:x=$\frac{\sqrt{3}}{2}$或x=-$\frac{\sqrt{3}}{2}$,
故答案为:x=$\frac{\sqrt{3}}{2}$或x=-$\frac{\sqrt{3}}{2}$.
点评 本题主要考查无理方程的求解,通过变形将无理方程化为整式方程是解题的关键.

练习册系列答案
相关题目
3.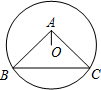 如图,⊙O过点B,C,圆心O在等腰直角△ABC的内部,∠BAC=90°,若OA=1,BC=6,则⊙O的半径为( )
如图,⊙O过点B,C,圆心O在等腰直角△ABC的内部,∠BAC=90°,若OA=1,BC=6,则⊙O的半径为( )
 如图,⊙O过点B,C,圆心O在等腰直角△ABC的内部,∠BAC=90°,若OA=1,BC=6,则⊙O的半径为( )
如图,⊙O过点B,C,圆心O在等腰直角△ABC的内部,∠BAC=90°,若OA=1,BC=6,则⊙O的半径为( )| A. | $\sqrt{10}$ | B. | 2$\sqrt{3}$ | C. | $\sqrt{13}$ | D. | 3$\sqrt{2}$ |
13.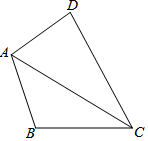 如图,四边形ABCD中,AB=AD,∠B+∠D=180°,若AC=12,则四边形ABCD的面积最大值为( )
如图,四边形ABCD中,AB=AD,∠B+∠D=180°,若AC=12,则四边形ABCD的面积最大值为( )
 如图,四边形ABCD中,AB=AD,∠B+∠D=180°,若AC=12,则四边形ABCD的面积最大值为( )
如图,四边形ABCD中,AB=AD,∠B+∠D=180°,若AC=12,则四边形ABCD的面积最大值为( )| A. | 36 | B. | $36\sqrt{2}$ | C. | 72 | D. | $72\sqrt{2}$ |
20.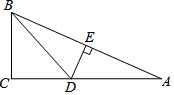 如图,在Rt△ABC中,∠C=90°,把AB对折后,点A与点B重合,折痕为DE,若BC=2,AC=4,则BD=( )
如图,在Rt△ABC中,∠C=90°,把AB对折后,点A与点B重合,折痕为DE,若BC=2,AC=4,则BD=( )
 如图,在Rt△ABC中,∠C=90°,把AB对折后,点A与点B重合,折痕为DE,若BC=2,AC=4,则BD=( )
如图,在Rt△ABC中,∠C=90°,把AB对折后,点A与点B重合,折痕为DE,若BC=2,AC=4,则BD=( )| A. | $\frac{3}{2}$ | B. | 2 | C. | $\frac{5}{2}$ | D. | 3 |
18.当(-6n)m=-6mn成立,则( )
| A. | m、n必须同时为正奇数 | B. | m、n必须同时为正偶数 | ||
| C. | m为奇数 | D. | m为偶数 |
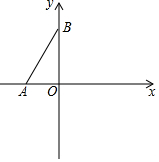 如图,点O为平面直角坐标系的原点,点A在x轴上,点B在y轴上,且AO=2,∠ABO=30°.
如图,点O为平面直角坐标系的原点,点A在x轴上,点B在y轴上,且AO=2,∠ABO=30°.