��Ŀ����
7�� ��ͼ����֪�����ϵ�A��B�������ϵ�һ�㣬AB=12������P�ӵ�A��������ÿ��6����λ���ȵ��ٶ����������������˶������˶�ʱ��Ϊt��t��0���룮
��ͼ����֪�����ϵ�A��B�������ϵ�һ�㣬AB=12������P�ӵ�A��������ÿ��6����λ���ȵ��ٶ����������������˶������˶�ʱ��Ϊt��t��0���룮��1��д�������ϵ�B��ʾ����Ϊ-4����t����P�߹���·��Ϊ6t���ú�t�Ĵ���ʽ��ʾ����
��2�����ڶ���P�˶���ͬʱ��һ����Q�ӵ�BҲ����������ÿ��4����λ���ȵ��ٶ����������������˶����ʾ�����ʱ���P�����ϵ�Q��
��3����MΪAP���е㣬NΪBP���е㣬��P���˶��Ĺ����У��߶�MN�ij����Ƿ����仯�����仯����˵�����ɣ������䣬���㻭��ͼ�Σ�������߶�MN�ij���
���� ��1�����B���ʾ����Ϊx���������������ľ��뼴�ɵõ�x�ķ��̣��ⷽ�̼��ɵó�x����·��=�ٶȡ�ʱ��ɵó���P�߹���·�̣�
��2���辭t���P����Q�㣬��������ɵã�����t��һԪһ�η��̣��ⷽ�̼��ɵó�ʱ��t��
��3����P��λ�õIJ�ͬ������������ǣ������е�Ķ��壬�����ҵ��߶μ�Ĺ�ϵ���Ӷ����ҳ�MN�ij��ȣ�
��� �⣺��1����B���ʾx������
AB=8-x=12�����x=-4��
�߶���P�ӵ�A��������ÿ��6����λ���ȵ��ٶ����������������˶���
�ྭt����P�߹���·��Ϊ6t��
�ʴ�Ϊ��-4��6t��
��2���辭t���P����Q�㣬��������ã�
6t-4t=12��
���t=6��
�𣺾���6��ʱ���P�����ϵ�Q��
��3������P���˶�������߶�MN������6��
���������������
�ٵ�P���߶�AB��ʱ����ͼ1��
MN=PM+PN=$\frac{1}{2}$PA+$\frac{1}{2}$PB=$\frac{1}{2}$��PA+PB��=$\frac{1}{2}$AB=$\frac{1}{2}$��12=6��
�ڵ�P���߶�AB���ӳ�����ʱ����ͼ2��
MN=PM-PN=$\frac{1}{2}$PA-$\frac{1}{2}$PB=$\frac{1}{2}$��PA-PB��=$\frac{1}{2}$AB=$\frac{1}{2}$��12=6��
���Ͽ�֪������P�˶�������߶�MN�ij��ȶ����䣬������6��
���� ���⿼�������ᡢ�е����ݽ�һԪһ�η��̣�����Ĺؼ��ǣ���1���ҳ�����x��һԪһ�η��̣���2���ҳ�����ʱ��t��һԪһ�η��̣���3�����е㶨���ҵ��߶μ�Ĺ�ϵ��

| A�� | 5�� | B�� | 6�� | C�� | 7�� | D�� | ������ |
 ��ͼ���ڱ߳�Ϊ1����λ���ȵ�С�����������У���A��B���Ǹ�㣨�������ߵĽ��㣩�����߶�AB�ij���Ϊ��������
��ͼ���ڱ߳�Ϊ1����λ���ȵ�С�����������У���A��B���Ǹ�㣨�������ߵĽ��㣩�����߶�AB�ij���Ϊ��������| A�� | 3$\sqrt{3}$ | B�� | 5 | C�� | 6 | D�� | 4$\sqrt{2}$ |
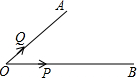 ��ͼ���ڡ�AOB=30���������������P��Q���˶����ҵ�P�����O��1����Զ�ĵط���������1����ÿ���˶�����Q�ӵ�O������2����ÿ���˶������POQΪ����������ʱ��������˶�ʱ��Ϊ���������룮
��ͼ���ڡ�AOB=30���������������P��Q���˶����ҵ�P�����O��1����Զ�ĵط���������1����ÿ���˶�����Q�ӵ�O������2����ÿ���˶������POQΪ����������ʱ��������˶�ʱ��Ϊ���������룮| A�� | $1��2\sqrt{3}+3��\frac{{2\sqrt{3}+1}}{11}$ | B�� | $1��2\sqrt{3}+3��\frac{{2\sqrt{3}+1}}{13}$ | C�� | $1��2\sqrt{3}+3$��5 | D�� | ���϶����� |
 ��ͼ�������̵صij�����������xm��
��ͼ�������̵صij�����������xm�� ��ͼ����Rt��ABO�У�����A��˫����y=$\frac{k}{x}$��ֱ��y=-x+��k+1���ڵ������Ľ��㣬AB��x����B��S��ABO=1.5��
��ͼ����Rt��ABO�У�����A��˫����y=$\frac{k}{x}$��ֱ��y=-x+��k+1���ڵ������Ľ��㣬AB��x����B��S��ABO=1.5�� ��ͼ����O�ǵȱߡ�ABC��һ�㣮��COB=140�㣬��AOB=��������COB�Ƶ�C��˳ʱ�뷽����ת60��á�ADC������OD
��ͼ����O�ǵȱߡ�ABC��һ�㣮��COB=140�㣬��AOB=��������COB�Ƶ�C��˳ʱ�뷽����ת60��á�ADC������OD