题目内容
14.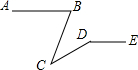 如图,AB∥DE,∠ABC=80°,∠BCD=40°,则∠CDE=140°.
如图,AB∥DE,∠ABC=80°,∠BCD=40°,则∠CDE=140°.
分析 延长ED交BC于点G,先根据平行线的性质求出∠FGC的度数,再由补角的定义得出∠CGD的度数,根据三角形外角的性质即可得出结论.
解答 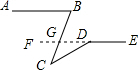 解:延长ED交BC于点G,
解:延长ED交BC于点G,
∵AB∥DE,∠ABC=80°,
∴∠FGC=80°,
∴∠CGD=180°-80°=100°.
∵∠CDE是△CDG的外角,
∴∠CDE=∠BCD+∠CGD=40°+100°=140°.
故答案为:140°.
点评 本题考查的是平行线的性质,用到的知识点为:两直线平行,同位角相等.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.若一个多边形的内角和等于1620°,则这个多边形的边数为( )
| A. | 9 | B. | 10 | C. | 11 | D. | 12 |
6.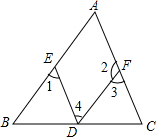 如图,在下列给出的条件中,不能判定AB∥DF的是( )
如图,在下列给出的条件中,不能判定AB∥DF的是( )
 如图,在下列给出的条件中,不能判定AB∥DF的是( )
如图,在下列给出的条件中,不能判定AB∥DF的是( )| A. | ∠A+∠2=180° | B. | ∠1=∠A | C. | ∠1=∠4 | D. | ∠A=∠3 |
 (1)解不等式组:$\left\{\begin{array}{l}{5-x>3}\\{\frac{x}{2}-\frac{2x-1}{3}-1≤0}\end{array}\right.$
(1)解不等式组:$\left\{\begin{array}{l}{5-x>3}\\{\frac{x}{2}-\frac{2x-1}{3}-1≤0}\end{array}\right.$
 如图所示,已知CD∥AB,OE平分∠DOB,OE⊥OF,∠CDO=60°,求∠DOF的度数.
如图所示,已知CD∥AB,OE平分∠DOB,OE⊥OF,∠CDO=60°,求∠DOF的度数.