题目内容
3. 如图所示,已知CD∥AB,OE平分∠DOB,OE⊥OF,∠CDO=60°,求∠DOF的度数.
如图所示,已知CD∥AB,OE平分∠DOB,OE⊥OF,∠CDO=60°,求∠DOF的度数.
分析 根据两直线平行内错角相等,得到∠D=∠AOD=60°,只要证明OF是∠AOD的角平分线即可.
解答  解:∵CD∥AB,
解:∵CD∥AB,
∴∠D=∠DOA=60°,
∵OE⊥OF,
∴∠EOF=90°,∠AOF+∠EOB=90°,
∵OE平分∠DOB,
∴∠DOE=∠EOB,
∵∠DOF+∠DOE=90°,∠AOF+∠EOB=90°,
∴∠DOF=∠AOF,
∴∠DOF=$\frac{1}{2}$∠DOA=$\frac{1}{2}$×60°=30°.
点评 本题考查平行线的性质、垂直的定义、等角的余角相等等知识,灵活运用这些知识是解题的关键,学会证明角相等的方法,属于中考常考题型.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.下列二次根式中,属于最简二次根式的是( )
| A. | $\sqrt{\frac{1}{2}}$ | B. | $\sqrt{5}$ | C. | $\sqrt{4}$ | D. | $\sqrt{0.8}$ |
11.∠1与∠2是直线a、b被直线c所截得的同位角,∠1与∠2的大小关系是( )
| A. | ∠1=∠2 | B. | ∠1>∠2 | C. | ∠1<∠2 | D. | 无法确定 |
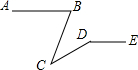 如图,AB∥DE,∠ABC=80°,∠BCD=40°,则∠CDE=140°.
如图,AB∥DE,∠ABC=80°,∠BCD=40°,则∠CDE=140°.
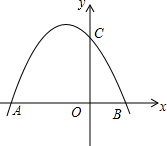 如图,已知抛物线y=ax2+bx+c与x轴交于点A(-6,0),B(2,0).
如图,已知抛物线y=ax2+bx+c与x轴交于点A(-6,0),B(2,0).
 =______.
=______.