题目内容
7.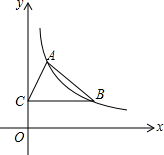 如图,反比例函数y=$\frac{k}{x}$(x>0)的图象经过点A(1,2)和点B(m,n),过点B作BC⊥y轴与C,若△ABC的面积为2,则点B的坐标为B(3,$\frac{2}{3}$).
如图,反比例函数y=$\frac{k}{x}$(x>0)的图象经过点A(1,2)和点B(m,n),过点B作BC⊥y轴与C,若△ABC的面积为2,则点B的坐标为B(3,$\frac{2}{3}$).
分析 根据三角形面积公式得到$\frac{1}{2}$•m•(2-n)=2,即2m-mn=4,再根据反比例函数图象上点的坐标特征得到mn=2,则可计算出m=3,n=$\frac{2}{3}$,从而可确定B点坐标.
解答 解:∵△ABC的面积为2,
∴$\frac{1}{2}$•m•(2-n)=2,
即2m-mn=4,
∵反比例函数y=$\frac{k}{x}$(x>0)的图象经过点A(1,2)和点B(m,n),
∴1×2=mn,
∴2m-2=4,解得m=3,
∴n=$\frac{2}{3}$,
∴B(3,$\frac{2}{3}$).
故答案为B(3,$\frac{2}{3}$).
点评 本题考查了反比例函数比例系数k的几何意义:在反比例函数y=$\frac{k}{x}$图象中任取一点,过这一个点向x轴和y轴分别作垂线,与坐标轴围成的矩形的面积是定值|k|.也考查了反比例函数图象上点的坐标特征.

练习册系列答案
相关题目
12.已知直角三角形的两直角边长分别是4和6,则其斜边长是( )
| A. | 4 | B. | 6 | C. | 10 | D. | 2$\sqrt{13}$ |
19.如图,AB=AC,BD=CD,若∠B=20°,则∠C的度数为( )

| A. | 30° | B. | 15° | C. | 20° | D. | 40° |
16.已知二次函数y=-x2+4x-a(a为常数)的图象与x轴的一个交点为(1,0),则关于x的一元二次方程-x2+4x-a=0的两实数根是( )
| A. | x1=1,x2=-1 | B. | x1=1,x2=2 | C. | x1=1,x2=0 | D. | x1=1,x2=3 |
 如图,线段AB的垂直平分线l交AB于C点,点P在l上,PA=5,AC=4,则△PAB的周长为18.
如图,线段AB的垂直平分线l交AB于C点,点P在l上,PA=5,AC=4,则△PAB的周长为18.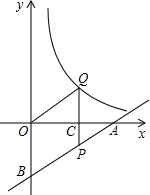 如图,一次函数y=$\frac{1}{2}$x-2的图象分别交x轴、y轴于A、B,P为AB上一点且PC为△AOB的中位线,PC的延长线交反比例函数y=$\frac{k}{x}$(k>0)的图象于Q,S△OQC=$\frac{3}{2}$,则k的值是3;Q点的坐标分别为(2,$\frac{3}{2}$).
如图,一次函数y=$\frac{1}{2}$x-2的图象分别交x轴、y轴于A、B,P为AB上一点且PC为△AOB的中位线,PC的延长线交反比例函数y=$\frac{k}{x}$(k>0)的图象于Q,S△OQC=$\frac{3}{2}$,则k的值是3;Q点的坐标分别为(2,$\frac{3}{2}$). )2·(-
)2·(- )=-
)=-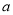 3 B.
3 B. 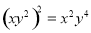 C.
C. 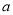 7÷
7÷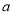 7=1 D. 2
7=1 D. 2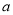 4·3
4·3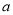 2=6
2=6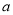 8
8 如图,直线AB⊥CD,垂足为O,射线OP在∠AOD的内部,且∠POA=4∠POD,则∠COP与∠BOP的比为3:2.
如图,直线AB⊥CD,垂足为O,射线OP在∠AOD的内部,且∠POA=4∠POD,则∠COP与∠BOP的比为3:2.