题目内容
19.(1)若$\sqrt{2x+3}$+$\frac{1}{x+1}$在实数范围内有意义,求x的取值范围.(2)在实数范围内分解下列因式:x2-3.
分析 (1)二次根式的被开方数是非负数,分式的分母不等于零;
(2)利用平方差公式进行因式分解.
解答 解:(1)依题意得:$\left\{\begin{array}{l}{2x+3≥0}\\{x+1≠0}\end{array}\right.$,
解得x≥-$\frac{3}{2}$,且x≠-1;
(2)x2-3=(x+$\sqrt{3}$)(x-$\sqrt{3}$).
点评 本题考查了分式有意义的条件和二次根式有意义的条件,以及实数范围内分解因式,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.若△ABC≌△DEF,∠A=∠D,∠C=∠F,且△ABC的周长为20,AB=5,BC=8,则DF长为( )
| A. | 5 | B. | 8 | C. | 7 | D. | 5或8 |
7.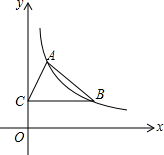 如图,反比例函数y=$\frac{k}{x}$(x>0)的图象经过点A(1,2)和点B(m,n),过点B作BC⊥y轴与C,若△ABC的面积为2,则点B的坐标为B(3,$\frac{2}{3}$).
如图,反比例函数y=$\frac{k}{x}$(x>0)的图象经过点A(1,2)和点B(m,n),过点B作BC⊥y轴与C,若△ABC的面积为2,则点B的坐标为B(3,$\frac{2}{3}$).
 如图,反比例函数y=$\frac{k}{x}$(x>0)的图象经过点A(1,2)和点B(m,n),过点B作BC⊥y轴与C,若△ABC的面积为2,则点B的坐标为B(3,$\frac{2}{3}$).
如图,反比例函数y=$\frac{k}{x}$(x>0)的图象经过点A(1,2)和点B(m,n),过点B作BC⊥y轴与C,若△ABC的面积为2,则点B的坐标为B(3,$\frac{2}{3}$).
7.下列图形中阴影部分的面积相等的是( )


| A. | ①② | B. | ②③ | C. | ③④ | D. | ①④ |
 画出将三角形ABC绕点O顺时针方向旋转90度后的对应三角形.(保留作图痕迹)
画出将三角形ABC绕点O顺时针方向旋转90度后的对应三角形.(保留作图痕迹)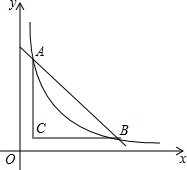 如图,将一块直角三角形纸板的直角顶点放在C(1,$\frac{1}{2}$),处,两直角边分别与x,y轴平行,纸板的另两个顶点A,B恰好是直线y=kx+$\frac{9}{2}$与双曲线y=$\frac{m}{x}$(m>0)的交点
如图,将一块直角三角形纸板的直角顶点放在C(1,$\frac{1}{2}$),处,两直角边分别与x,y轴平行,纸板的另两个顶点A,B恰好是直线y=kx+$\frac{9}{2}$与双曲线y=$\frac{m}{x}$(m>0)的交点 一张矩形纸片ABCD的边长分别为9厘米和3厘米,把顶点A和C叠合在一起,得到折痕EF.
一张矩形纸片ABCD的边长分别为9厘米和3厘米,把顶点A和C叠合在一起,得到折痕EF.