题目内容
14. 如图,直线AB⊥CD,垂足为O,射线OP在∠AOD的内部,且∠POA=4∠POD,则∠COP与∠BOP的比为3:2.
如图,直线AB⊥CD,垂足为O,射线OP在∠AOD的内部,且∠POA=4∠POD,则∠COP与∠BOP的比为3:2.
分析 利用垂直的定义得出∠COA=∠AOD=∠BOD=90°,进而得出∠POA=72°,∠POD=18°,再求出∠COP与∠BOP的比.
解答 解:∵直线AB⊥CD,垂足为O,
∴∠COA=∠AOD=∠BOD=90°,
∵∠POA=4∠POD,
∴∠POA=72°,∠POD=18°,
∴∠COP=90°+72°=162°,
∠BOP=90°+18°=108°,
∴∠COP与∠BOP的比为:3:2.
故答案为:3:2.
点评 此题主要考查了垂线的定义,根据题意得出∠COP与∠BOP的度数是解题关键.

练习册系列答案
相关题目
7.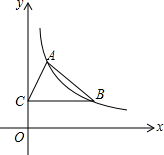 如图,反比例函数y=$\frac{k}{x}$(x>0)的图象经过点A(1,2)和点B(m,n),过点B作BC⊥y轴与C,若△ABC的面积为2,则点B的坐标为B(3,$\frac{2}{3}$).
如图,反比例函数y=$\frac{k}{x}$(x>0)的图象经过点A(1,2)和点B(m,n),过点B作BC⊥y轴与C,若△ABC的面积为2,则点B的坐标为B(3,$\frac{2}{3}$).
 如图,反比例函数y=$\frac{k}{x}$(x>0)的图象经过点A(1,2)和点B(m,n),过点B作BC⊥y轴与C,若△ABC的面积为2,则点B的坐标为B(3,$\frac{2}{3}$).
如图,反比例函数y=$\frac{k}{x}$(x>0)的图象经过点A(1,2)和点B(m,n),过点B作BC⊥y轴与C,若△ABC的面积为2,则点B的坐标为B(3,$\frac{2}{3}$).
7.下列图形中阴影部分的面积相等的是( )


| A. | ①② | B. | ②③ | C. | ③④ | D. | ①④ |
9.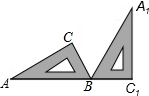 如图,将三角尺ABC(其中∠ABC=60°,∠C=90°)绕B点按顺时针方向旋转一个角度到A1B1C1的位置,使得点A,B,C1在同一条直线上,那么这个角度等于( )
如图,将三角尺ABC(其中∠ABC=60°,∠C=90°)绕B点按顺时针方向旋转一个角度到A1B1C1的位置,使得点A,B,C1在同一条直线上,那么这个角度等于( )
 如图,将三角尺ABC(其中∠ABC=60°,∠C=90°)绕B点按顺时针方向旋转一个角度到A1B1C1的位置,使得点A,B,C1在同一条直线上,那么这个角度等于( )
如图,将三角尺ABC(其中∠ABC=60°,∠C=90°)绕B点按顺时针方向旋转一个角度到A1B1C1的位置,使得点A,B,C1在同一条直线上,那么这个角度等于( )| A. | 30° | B. | 60° | C. | 90° | D. | 120° |
4.下列是二元一次方程的是( )
| A. | 3x=10 | B. | 2x2=y | C. | y+$\frac{1}{x}$=2 | D. | x+8y=0 |
 按要求分别解这个方程:①配方法;②因式分解法.
按要求分别解这个方程:①配方法;②因式分解法.