题目内容
16.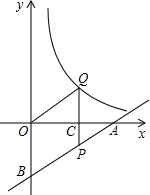 如图,一次函数y=$\frac{1}{2}$x-2的图象分别交x轴、y轴于A、B,P为AB上一点且PC为△AOB的中位线,PC的延长线交反比例函数y=$\frac{k}{x}$(k>0)的图象于Q,S△OQC=$\frac{3}{2}$,则k的值是3;Q点的坐标分别为(2,$\frac{3}{2}$).
如图,一次函数y=$\frac{1}{2}$x-2的图象分别交x轴、y轴于A、B,P为AB上一点且PC为△AOB的中位线,PC的延长线交反比例函数y=$\frac{k}{x}$(k>0)的图象于Q,S△OQC=$\frac{3}{2}$,则k的值是3;Q点的坐标分别为(2,$\frac{3}{2}$).
分析 先根据坐标轴上点的坐标特征求出A(4,0),再根据三角形中位线性质得PC∥OB,C(2,0),接着根据反比例函数系数k的几何意义得到$\frac{1}{2}$|k|=$\frac{3}{2}$,可解得k=3,则反比例函数解析式为y=$\frac{3}{x}$,由于Q点的横坐标为2,则计算出x=2时,y=$\frac{3}{2}$,于是得到Q点的坐标为(2,$\frac{3}{2}$).
解答 解:当y=0时,$\frac{1}{2}$x-2=0,解得x=4,则A(4,0),
∵PC为△AOB的中位线,
∴PC∥OB,C(2,0),
∵S△OQC=$\frac{1}{2}$|k|=$\frac{3}{2}$,
而k>0,
∴k=3,
∴反比例函数解析式为y=$\frac{3}{x}$,
当x=2时,y=$\frac{3}{2}$,
∴Q点的坐标为(2,$\frac{3}{2}$).
故答案为3,(2,$\frac{3}{2}$).
点评 本题考查了反比例函数比例系数k的几何意义:在反比例函数y=$\frac{k}{x}$图象中任取一点,过这一个点向x轴和y轴分别作垂线,与坐标轴围成的矩形的面积是定值|k|.也考查了三角形中位线性质.

练习册系列答案
 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
 画出将三角形ABC绕点O顺时针方向旋转90度后的对应三角形.(保留作图痕迹)
画出将三角形ABC绕点O顺时针方向旋转90度后的对应三角形.(保留作图痕迹) 一张矩形纸片ABCD的边长分别为9厘米和3厘米,把顶点A和C叠合在一起,得到折痕EF.
一张矩形纸片ABCD的边长分别为9厘米和3厘米,把顶点A和C叠合在一起,得到折痕EF.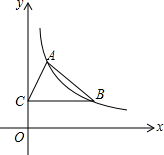 如图,反比例函数y=$\frac{k}{x}$(x>0)的图象经过点A(1,2)和点B(m,n),过点B作BC⊥y轴与C,若△ABC的面积为2,则点B的坐标为B(3,$\frac{2}{3}$).
如图,反比例函数y=$\frac{k}{x}$(x>0)的图象经过点A(1,2)和点B(m,n),过点B作BC⊥y轴与C,若△ABC的面积为2,则点B的坐标为B(3,$\frac{2}{3}$).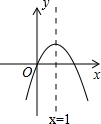 二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:(1)b>0;(2)c>0;(3)4a+2b+c>0;(4)(a+b)2<b2,其中正确的有( )
二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:(1)b>0;(2)c>0;(3)4a+2b+c>0;(4)(a+b)2<b2,其中正确的有( ) 按要求分别解这个方程:①配方法;②因式分解法.
按要求分别解这个方程:①配方法;②因式分解法.