题目内容
12．函数y=$\sqrt{1-2x}$的最小值是0．分析 利用二次根式的有意义的条件进而分析得出函数最小值．
解答 解：∵$\sqrt{1-2x}$有意义，
∴1-2x≥0，
∴函数y=$\sqrt{1-2x}$的最小值是：$\sqrt{1-2x}$=0．
故答案为：0．
点评 此题主要考查了无理函数的最值，结合二次根式的性质分析得出是解题关键．
练习册系列答案
相关题目
2．如果x2-4xy+4y2=0，那么$\frac{x-y}{x+y}$的值等于（ ）
| A． | -$\frac{1}{3}$ | B． | -$\frac{1}{3y}$ | C． | $\frac{1}{3}$ | D． | $\frac{1}{3y}$ |
3．某玩具工厂只生产两种玩具：小狗和小汽车，工人小王的生产记录如表：
若小王某天工作了八小时，问他这天最多挣多少钱？（工厂对小王这天生产何种产品无限制、只有成品才有工资）
| 玩具小狗件数（单位：个） | 玩具小汽车个数（单位：个） | 总时间（单位：分） | 总工资（单位：元） |
| 1 | 1 | 35 | 2.15 |
| 2 | 2 | 70 | 4.30 |
| 3 | 2 | 85 | 5.05 |
20．如图所示的四个函数图象中，y随x的增大而增大的是（ ）
| A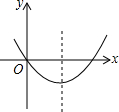． |  | B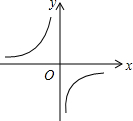． |  | C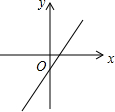． |  | D． |  |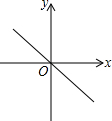
已知直角三角形面积是8平方厘米，求阴影部分面积．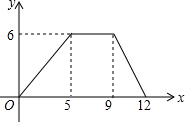
如图，是一对变量满足的函数关系的图象．有下列3个不同的问题情境：