题目内容
7．在直角坐标系中，点A、B的坐标分别为（-2，4）、（-5，2），点M是x轴上的点，点N是y轴上的点，如果以点A、B、M、N为顶点的四边形是平行四边形，那么符合条件的点M有（ ）| A． | 1 | B． | 2 | C． | 3 | D． | 4 |
分析 根据“一组对边相等且平行的四边形是平行四边形”即可得出答案．
解答 解：如图所示：
当AB平行且等于N1M1时，四边形ABM1N1是平行四边形；
当AB平行且等于N2M2时，四边形ABN2M2是平行四边形；
当AB为对角线时，四边形AN3BM3是平行四边形．
故符合题意的有3个点．
故选：C．
点评 此题考查了平行四边形的判定；结合AB的长分别确定M，N的位置是解决问题的关键．
练习册系列答案
相关题目
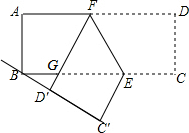如图，矩形ABCD中，AB=4，AD=9，点E、F分别是BC、AD上的动点，∠FEC为钝角，沿直线EF翻折矩形，点C、D的对应点分别为C′、D′，若C′、D′、B在同一条直线上，且$\frac{BD′}{BC′}$=$\frac{1}{3}$时，则AF的长为3$\frac{5}{6}$．
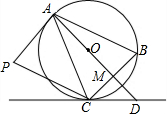如图，AP是⊙O的切线，A为切点，AB是⊙O的弦，过点B作BC∥AP，交⊙O于点C，连接AC，过点C作CP∥AP于点P，连接AO并延长，交BC于点M，交过点C的直线于点D，且∠ACP=∠BCD
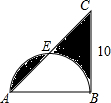求图中阴影部分的面积，E是Rt△ABC斜边AC的中点．
16．若xy≠1，且有7x2+2009x+13=0及13y2+2009y+7=0，则$\frac{x}{y}$的值是（ ）
| A． | $\frac{13}{7}$ | B． | $\frac{7}{13}$ | C． | -$\frac{2009}{7}$ | D． | -$\frac{2009}{13}$ |
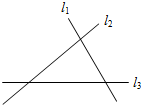如图所示，直线l1，l2，l3表示三条相交的公路，现要建一个货物中转站，要求它到三条公路的距离相等，则可供选择的地址有（ ）