题目内容
17. 已知直角三角形面积是8平方厘米,求阴影部分面积.
已知直角三角形面积是8平方厘米,求阴影部分面积.
分析 连接OD,由△ABC是直角三角形,∠B=45°,得到△ABC是等腰直角三角形,根据其面积=8,求得BC=4,于是得到S弓形=S扇形BOD-S△BOD=$\frac{90π•{2}^{2}}{360}$-$\frac{1}{2}$×2×2=π-2,则即可得到结论S阴影.
解答 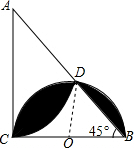 解:如图,连接OD,
解:如图,连接OD,
∵△ABC是直角三角形,∠B=45°,
∴AC=BC,
∵△ABC的面积=8,
∴BC=4,
∴S弓形=S扇形BOD-S△BOD=$\frac{90π•{2}^{2}}{360}$-$\frac{1}{2}$×2×2=π-2,
∴S阴影=3S弓形=3π-6.
点评 本题考查了等腰直角三角形的性质,三角形面积的求法,扇形的面积,知道把不规则的图形转化为规则图形来计算是解题的关键.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
8.若化简|2-x|-$\sqrt{{x}^{2}-8x+16}$的结果是-2,则x的取值范围是( )
| A. | x为任意实数 | B. | 2≤x≤4 | C. | x≥4 | D. | x≤2 |
6.有5条线段长度分别为1,3,4,5,7,从中任取三条为一组,它们一定能构成三角形的频率为( )
| A. | 0.15 | B. | 0.10 | C. | 0.20 | D. | 0.30 |
 一束光线经三块平面镜AB,CD,EF反射的路线如图所示,∠MEN=110°,∠1=60°.
一束光线经三块平面镜AB,CD,EF反射的路线如图所示,∠MEN=110°,∠1=60°.