��Ŀ����
3�� ��ͼ����֪������y=-$\frac{1}{4}$x2+bx+4��x���ཻ��A��B���㣬��y���ཻ�ڵ�C������֪B�������ΪB��8��0��
��ͼ����֪������y=-$\frac{1}{4}$x2+bx+4��x���ཻ��A��B���㣬��y���ཻ�ڵ�C������֪B�������ΪB��8��0����1���������ߵĽ���ʽ����Գ��ᣮ
��2������AC��BC�����жϡ�AOC���COB�Ƿ����ƣ���˵�����ɣ�
��3��MΪ��������BC֮���һ�㣬NΪ�߶�BC�ϵ�һ�㣬��MN��y�ᣬ��MN�����ֵ��
��4���������ߵĶԳ������Ƿ���ڵ�Q��ʹ��ACQΪ���������Σ������ڣ��������������Q�����ꣻ�������ڣ���˵�����ɣ�
���� ��1���ѵ�B��������������߽���ʽ���b��ֵ�����ɵõ������߽���ʽ���ٸ��ݶԳ��᷽����ʽ���㼴�ɵý⣻
��2����y=0���ⷽ�������A�����꣬��x=0���y��ֵ�õ���C�����꣬�����OA��OB��OC��Ȼ����ݶ�Ӧ�߳ɱ������н���ȵ���������������֤����
��3����ֱ��BC�Ľ���ʽΪy=kx+b�����ô���ϵ�����������ʽ���ٱ�ʾ��MN��Ȼ����ݶ��κ�������ֵ������
��4�����ù��ɶ�����ʽ���AC������C��CD�ͶԳ�����D��Ȼ��֢�AC=CQʱ�����ù��ɶ�����ʽ���DQ���ֵ�Q�ڵ�D���Ϸ����·�������������Q��x��ľ��룬��д��������꼴�ɣ��ڵ�QΪ�Գ�����x��Ľ���ʱ��AQ=CQ����д����Q�����꼴�ɣ�
��� �⣺��1���ߵ�B��8��0����������y=-$\frac{1}{4}$x2+bx+4�ϣ�
��-$\frac{1}{4}$��64+8b+4=0��
��ã�b=$\frac{3}{2}$��
�������ߵĽ���ʽΪy=-$\frac{1}{4}$x2+$\frac{3}{2}$x+4��
�Գ���Ϊֱ��x=-$\frac{\frac{3}{2}}{2����-\frac{1}{4}��}$=3��
��2����AOC�ס�COB��
�������£���y=0����-$\frac{1}{4}$x2+$\frac{3}{2}$x+4=0��
��x2-6x-16=0��
��ã�x1=-2��x2=8��
���A��������-2��0����
��x=0����y=4��
���C��������0��4����
��OA=2��OB=8��OC=4��
��$\frac{OC}{OA}$=$\frac{OB}{OC}$=2����AOC=��COB=90�㣬
���AOC�ס�COB��
��3����ֱ��BC�Ľ���ʽΪy=kx+b��
��$\left\{\begin{array}{l}{8k+b=0}\\{b=4}\end{array}\right.$��
��ã�$\left\{\begin{array}{l}{k=-\frac{1}{2}}\\{b=4}\end{array}\right.$��
��ֱ��BC�Ľ���ʽΪy=-$\frac{1}{2}$x+4��
��MN��y�ᣬ
��MN=-$\frac{1}{4}$x2+$\frac{3}{2}$x+4-��-$\frac{1}{2}$x+4����
=-$\frac{1}{4}$x2+$\frac{3}{2}$x+4+$\frac{1}{2}$x-4��
=-$\frac{1}{4}$x2+2x��
=-$\frac{1}{4}$��x-4��2+4��
�൱x=4ʱ��MN��ֵ������ֵΪ4��
��4���ɹ��ɶ����ã�AC=$\sqrt{{2}^{2}+{4}^{2}}$=2$\sqrt{5}$��
����C��CD�ͶԳ�����D����CD=3��
��AC=CQʱ��DQ=$\sqrt{C{Q}^{2}-C{D}^{2}}$=$\sqrt{��2\sqrt{5}��^{2}-{3}^{2}}$=$\sqrt{11}$��
��Q�ڵ�D���Ϸ�ʱ����Q��x��ľ���Ϊ4+$\sqrt{11}$��
��ʱ��Q1��3��4+$\sqrt{11}$����
��Q�ڵ�D���·�ʱ����Q��x��ľ���Ϊ4-$\sqrt{11}$��
��ʱ��Q2��3��4-$\sqrt{11}$����
�ڵ�QΪ�Գ�����x��Ľ���ʱ��AQ=5��
CQ=$\sqrt{{3}^{2}+{4}^{2}}$=5��
��AQ=CQ��
��ʱ����Q3��3��0����
�۵�AC=AQʱ����AC=2$\sqrt{5}$����A���Գ���ľ���Ϊ5��2$\sqrt{5}$��5��
���������β����ڣ�
������������Q������Ϊ��3��4+$\sqrt{11}$����3��4-$\sqrt{11}$����3��0��ʱ����ACQΪ���������Σ�
���� �����Ƕ��κ����ۺ����ͣ���Ҫ�����˴���ϵ��������κ�������ʽ������ϵ������һ�κ�������ʽ�����������ε��ж������κ�������ֵ���⣬���ɶ�����Ӧ�ã����������ε����ʣ��ѵ����ڣ�4��Ҫ��������ۣ�

 53���ò�ϵ�д�
53���ò�ϵ�д�| A�� | $\sqrt{16}$=��4 | B�� | 3-2=-$\frac{1}{9}$ | C�� | ��$\sqrt{3}-\sqrt{2}$��2=1 | D�� | ��$\sqrt{2}$-1��0=1 |
 ��ͼ��AB�ǡ�O���ң��뾶OC��AB�ڵ�D������O�İ뾶Ϊ5��AB=8����CD�ij���2��
��ͼ��AB�ǡ�O���ң��뾶OC��AB�ڵ�D������O�İ뾶Ϊ5��AB=8����CD�ij���2�� ��֪��ͼ�����ı���ABCD�У�AD��BC��BC��AD��BDƽ�֡�ABC��E��F�ֱ���BD��AC���е㣮��֤��
��֪��ͼ�����ı���ABCD�У�AD��BC��BC��AD��BDƽ�֡�ABC��E��F�ֱ���BD��AC���е㣮��֤�� ��ͼ���ڱ߳�Ϊ2������ABCD�У���ABC=120�㣬E��F�ֱ�ΪAD��CD�ϵĶ��㣬��AE+CF=2�����߶�EF������Сֵ��$\sqrt{3}$��
��ͼ���ڱ߳�Ϊ2������ABCD�У���ABC=120�㣬E��F�ֱ�ΪAD��CD�ϵĶ��㣬��AE+CF=2�����߶�EF������Сֵ��$\sqrt{3}$��
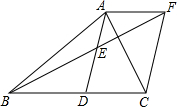 ��֪���ڡ�ABC�У�AD��BC���ϵ����ߣ���E��AD���е㣻����A��AF��BC����BE���ӳ�����F������CF��
��֪���ڡ�ABC�У�AD��BC���ϵ����ߣ���E��AD���е㣻����A��AF��BC����BE���ӳ�����F������CF��