题目内容
13．（1）1×2×3×4+1=（25）=（5）2；（2）2×3×4×5+1=（121）=（11）2；
（3）3×4×5×6+1=（361）=（19）2；
…
（4）猜测四个款项正整数的积加上1一定是n（n+1）（n+2）（n+3）+1=[n（n+3）]2+1．．
请用学习过的因式分解证明以上结论．
分析 由题意可知：连续四个自然数的乘积加1，结果等于两端的自然数乘积加1的平方，由此规律得出第n个等式为n（n+1）（n+2）（n+3）+1=[n（n+3）]2+1．进一步利用因式分解得出答案即可．
解答 解：（1）1×2×3×4+1=25=52；
（2）2×3×4×5+1=121=112；
（3）3×4×5×6+1=361=192；
…
（4）第n个等式为n（n+1）（n+2）（n+3）+1=[n（n+3）+1]2．
证明：左边=[n（n+3）][（n+1）（n+2）]+1
=（n2+3n）（n2+3n+2）+1
=（n2+3n）+2（n2+3n）+1
=[n（n+3）+1]2．
点评 此题考查因式分解的实际运用，发现数字的运算规律，掌握完全平方公式是解决问题的关键．
练习册系列答案
全优冲刺100分系列答案
英才点津系列答案
红果子三级测试卷系列答案
相关题目
4．
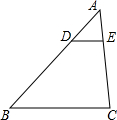如图，在△ABC中，DE∥BC，$\frac{AD}{DB}=\frac{1}{2}$，则下列结论中正确的是（ ）
如图，在△ABC中，DE∥BC，$\frac{AD}{DB}=\frac{1}{2}$，则下列结论中正确的是（ ）| A． | $\frac{AE}{EC}=\frac{1}{2}$ | B． | $\frac{DE}{BC}=\frac{1}{2}$ | ||
| C． | $\frac{△ADE的周长}{△ABC的周长}=\frac{1}{2}$ | D． | $\frac{△ADE的面积}{△ABC的面积}=\frac{1}{3}$ |