题目内容
6.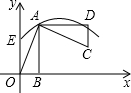 如图,抛物线y=ax2+$\frac{7}{5}$x+c经过点A(2,4),E(0,2),AB⊥x轴于点B.
如图,抛物线y=ax2+$\frac{7}{5}$x+c经过点A(2,4),E(0,2),AB⊥x轴于点B.(1)求该抛物线的表达式;
(2)将△ABO绕点A逆时针旋转90°得到△ADC,写出DC的中点P的坐标,试判断点P是否在此抛物线上,并说明理由.
分析 (1)将点A(2,4),E(0,2),代入解析式y=ax2+$\frac{7}{5}$x+c得到关于a、c方程组,解方程组可得;
(2)根据旋转性质可得点D、点C及点P的坐标,将点P坐标代入可知.
解答 解:(1)将点A(2,4),E(0,2),代入解析式y=ax2+$\frac{7}{5}$x+c,
得:$\left\{\begin{array}{l}{4a+\frac{14}{5}+c=4}\\{c=2}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=-\frac{1}{5}}\\{c=2}\end{array}\right.$,
故抛物线解析式为:y=-$\frac{1}{5}$x2+$\frac{7}{5}$x+2;
(2)由题意可知,AB=4,BO=2,
∵△ADC是由△ABO绕点A逆时针旋转90°得到,
∴AD=AB=4,CD=OB=2,
则点D坐标为(6,4),点C坐标为(6,2),
∴DC中点P的坐标为(6,3),
在y=-$\frac{1}{5}$x2+$\frac{7}{5}$x+2中,当x=6时,y=-$\frac{1}{5}$×62+$\frac{7}{5}$×6+2=$\frac{16}{5}$≠3,
故点P不在抛物线上.
点评 本题主要考查待定系数法求抛物线解析式及坐标与图形的变化,待定系数法求出抛物线解析式是解题的根本,根据旋转性质求得点的坐标是关键.

练习册系列答案
 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
15.小明的哥哥是一名大学生,他利用暑假去一家公司打工,报酬按16元/时计算,设小明的哥哥这个月工作的时间为t小时,应得报酬为m元,填写下表后回答下列问题:
(1)在上述问题中,哪些是常量?哪些是变量?
(2)能用含t的代数式来表示m的值吗?
| 工作时间t(小时) | 1 | 5 | 10 | 15 | 20 | … |
| 报酬m元 | 16 | 80 | 160 | 240 | 320 |
(2)能用含t的代数式来表示m的值吗?
 已知:△ABC
已知:△ABC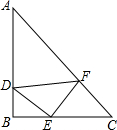 如图,△ABC、△DEF都是等腰三角形,D、E、F分别在AB、BC、CA上,已知:∠B=∠DEF=90°,AB=BC,DE=EF.
如图,△ABC、△DEF都是等腰三角形,D、E、F分别在AB、BC、CA上,已知:∠B=∠DEF=90°,AB=BC,DE=EF. 如图是“宝真商场”中某洗发水的价格标签,那么这种洗发水的原价是24元.
如图是“宝真商场”中某洗发水的价格标签,那么这种洗发水的原价是24元.