题目内容
14.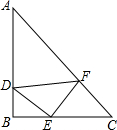 如图,△ABC、△DEF都是等腰三角形,D、E、F分别在AB、BC、CA上,已知:∠B=∠DEF=90°,AB=BC,DE=EF.
如图,△ABC、△DEF都是等腰三角形,D、E、F分别在AB、BC、CA上,已知:∠B=∠DEF=90°,AB=BC,DE=EF.(1)写出图中所有与∠BDE相等的角;
(2)求证:BD+BE=EC.
分析 (1)结合等腰三角形的性质,结合“同角的余角相等”即可判断;
(2)过点F作FG⊥BC,证明三角形BDE与三角形GEF全等即可.
解答 (1)解:图中与∠BDE相等的角有:∠FEC,∠AFD;
(2)证明:如图1,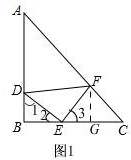
过点F作FG⊥BC与点G,
∵△ABC、△DEF都是等腰三角形,
∴∠B=∠EGF,DE=EF,
∴∠1+∠2=∠2+∠3=90°,
∴∠1=∠3,
在△DBE和△EGF中,
$\left\{\begin{array}{l}{∠1=∠3}\\{∠B=∠EGF}\\{DE=FE}\end{array}\right.$,
∴△DBE≌△EGF,
∴BD=EG,BE=FG,
∵∠C=∠CFG=45°,
∴FG=GC,
∴BD+BE=EG+GC=EC.
点评 此题主要考查全等三角形的判定与运用,会根据题意构造全等三角形解决问题是解题的关键.

练习册系列答案
 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案 培优三好生系列答案
培优三好生系列答案
相关题目
5.在-(-8),-|-7|,-|0|,(-2)2,-32这四个数中,非负数共有( )
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
2.在下列实数中,无理数是( )
| A. | 3.1415926 | B. | $\frac{22}{7}$ | C. | $\sqrt{3}$ | D. | $\sqrt{\frac{4}{9}}$ |
19.下列说法中正确的是( )
| A. | x的系数是0 | B. | y的次数是0 | ||
| C. | 23xy是二次单项式 | D. | 32与42不是同类项 |
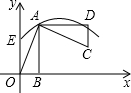 如图,抛物线y=ax2+$\frac{7}{5}$x+c经过点A(2,4),E(0,2),AB⊥x轴于点B.
如图,抛物线y=ax2+$\frac{7}{5}$x+c经过点A(2,4),E(0,2),AB⊥x轴于点B.