题目内容
如图.在△ABC中,BC>AC,点D在BC上,且DC=AC,∠ACB的平分线CF交AD于点F,点E是AB的中点,连接EF.
(1)求证:EF∥BC;
(2)若四边形BDFE的面积为6,求△ABD的面积.

(1)证明:∵DC=AC,∠ACB的平分线CF交AD于F,
∴F为AD的中点,
∵点E是AB的中点,
∴EF为△ABD的中位线,
∴EF∥BC;
(2)解:∵EF为△ABD的中位线,
∴ ,EF∥BD,
,EF∥BD,
∴△AEF∽△ABD,
∴S△AEF:S△ABD=1:4,
∴S△AEF:S四边形BDFE=1:3,
∵四边形BDFE的面积为6,
∴S△AEF=2,
∴S△ABD=S△AEF+S四边形BDFE=2+6=8.

练习册系列答案
 优等生题库系列答案
优等生题库系列答案
相关题目

 G,且菱形AEFG∽菱形ABCD,连接EB,GD.
G,且菱形AEFG∽菱形ABCD,连接EB,GD. ,求GD的长.
,求GD的长.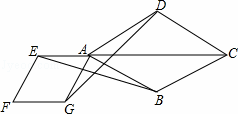

 BC,
BC,
 B.3
B.3 C.
C.

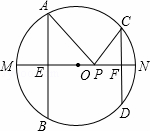

 ,AD=1.求BC的长.
,AD=1.求BC的长.