题目内容
如图,点E是菱形ABCD对角线CA的延长线上任意一点,以线段AE为边作一个菱形AEF G,且菱形AEFG∽菱形ABCD,连接EB,GD.
G,且菱形AEFG∽菱形ABCD,连接EB,GD.
(1)求证:EB=GD;
(2)若∠DAB=60°,AB=2,AG=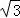 ,求GD的长.
,求GD的长.
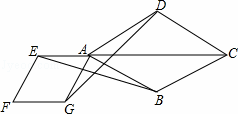
(1)证明:∵菱形AEFG∽菱形ABCD,
∴∠EAG=∠BAD,
∴∠EAG+∠GAB=∠BAD+∠GAB,
∴∠EAB=∠GAD,
∵AE=AG,AB=AD,
∴△AEB≌△AGD,
∴EB=GD;
(2)解:连接BD交AC于点P,则BP⊥AC,
∵∠DAB=60°,
∴∠PAB=30°,
∴BP= AB=1,
AB=1,
AP= =
= ,AE=AG=
,AE=AG= ,
,
∴EP=2 ,
,
∴EB= =
= =
= ,
,
∴GD= .
.


练习册系列答案
相关题目
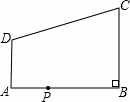

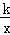 (k≠0)在第一象限的图象经过OA的中点B,交AC于点D,连接OD.若△OCD∽△ACO,则直线OA的解析式为 .
(k≠0)在第一象限的图象经过OA的中点B,交AC于点D,连接OD.若△OCD∽△ACO,则直线OA的解析式为 .
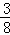 AC,AB=10时,求线段BO的长度.
AC,AB=10时,求线段BO的长度.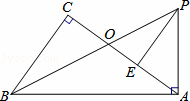
 D. 2:1
D. 2:1