题目内容
12.在△ABC中,AC=BC,∠ACB=90°,点D在直线AC上,连接BD,过点A作直线BD的垂线,垂足为E,直线AE与直线BC交于点F.(1)当点D在线段AC上时,如图1,求证:AD+CF=BC;
(2)当点D在AC的延长线上时,过点E作EH⊥AB于H,连接CH,如图2,若∠CBD=15°,AH=3,求△BCH的面积.

分析 (1)根据已知条件证明△BCD≌△ACF,得到CD=CF,所以AD+CF=AD+CD=AC=BC,即AD+CF=BC.
(2)根据∠CBD=15°,∠ABC=45°,得到∠ABE=60°,∠BAE=30°,利用在直角三角形AHE中 $\frac{EH}{AH}$=tan30° 得EH=$\sqrt{3}$EA=2$\sqrt{3}$,在直角三角形EHB中,$\frac{HB}{EH}$=tan30°,得BH=1,AB=BH+HA=4,在直角三角形ACB中,$\frac{AC}{AB}$=sin45°得AC=BC=2$\sqrt{2}$,如图2,过C做垂线CG垂直AB于G,求得得CG=2,即可得到三角形CHB面积为$\frac{1}{2}•GC•HB$=$\frac{1}{2}×2×1$=1.
解答 解:(1)当D在线段AC上时,
∵BC垂直DC于C点,AE垂直DE于E点,
∴∠BCA=∠AED=90°,
∵∠ADE=∠BDC,
∴∠EAD=∠CBD,
在△BCD和△ACF中,
$\left\{\begin{array}{l}{∠EAD=∠DBC}\\{AC=BC}\\{∠ACF=∠BCD=9{0}^{°}}\end{array}\right.$
∴△BCD≌△ACF,
∴CD=CF,
∴AD+CF=AD+CD=AC=BC,
即AD+CF=BC.
(2)∵∠CBD=15°,∠ABC=45°,
∴∠ABE=60°,∠BAE=30°,
∴在直角三角形AHE中 $\frac{EH}{AH}$=tan30°
得EH=$\sqrt{3}$EA=2$\sqrt{3}$,
在直角三角形EHB中,$\frac{HB}{EH}$=tan30°
得BH=1,
AB=BH+HA=4
在直角三角形ACB中,$\frac{AC}{AB}$=sin45°
得AC=BC=2$\sqrt{2}$,
如图2,过C作垂线CG垂直AB于G,
在直角三角形CGB中,$\frac{CG}{CB}$=sin45°
得CG=2,
∴三角形CHB,面积为$\frac{1}{2}•GC•HB$=$\frac{1}{2}×2×1$=1.
点评 本题考查了全等三角形的性质与判定,三角函数的应用,在(1)中解决问题的关键是证明△BCD≌△ACF,在(2)中解决问题的关键是利用三角函数求得三角形的边长.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案①如果地面向上15米记作15米,那么地面向下6米记作-6米;②一个有理数不是正数就是负数;③正数与负数是互为相反数;④任何一个有理数的绝对值都不可能小于零.
| A. | ①,② | B. | ②,③ | C. | ③,④ | D. | ④,① |
| A. | 若a2=b2,则a=b | B. | 若a>b,则a2>b2 | ||
| C. | 若a≠0,b≠0,则a2+b2>0 | D. | 若a≠b,则a2≠b2 |
 如图,已知BE⊥AC于点E,DE⊥AC于点F,BE=DF,AE=CF,求证:AB∥CD.
如图,已知BE⊥AC于点E,DE⊥AC于点F,BE=DF,AE=CF,求证:AB∥CD. 汽车油箱中原有油50升,如果行驶中每小时用油5升,求油箱的油量y(单位:升)随行驶时间x(单位:时)变化的函数关系式,并写出自变量x的取值范围.
汽车油箱中原有油50升,如果行驶中每小时用油5升,求油箱的油量y(单位:升)随行驶时间x(单位:时)变化的函数关系式,并写出自变量x的取值范围. 如图,三个正方形拼成一个矩形ABEF.
如图,三个正方形拼成一个矩形ABEF.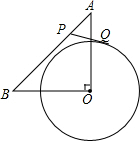 如图,在Rt△AOB中,OA=OB=3$\sqrt{2}$,⊙O的半径为2,点P是AB边上一动点,过P作⊙O的一条切线,切点为Q,求PQ的最小值和最大值.
如图,在Rt△AOB中,OA=OB=3$\sqrt{2}$,⊙O的半径为2,点P是AB边上一动点,过P作⊙O的一条切线,切点为Q,求PQ的最小值和最大值.