题目内容
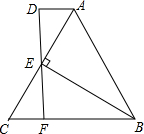 如图,已知△ABC,过A点作过AD∥BC,DF和AC交于E点,且AD=CF,连BE
如图,已知△ABC,过A点作过AD∥BC,DF和AC交于E点,且AD=CF,连BE(1)证明:E是DF中点;
(2)若BE⊥AC,∠C=60°,证明:△ABC是等边三角形.
考点:全等三角形的判定与性质
专题:证明题
分析:(1)易证△ADE≌△CFE,根据全等三角形对应边相等可解题;
(2)根据垂直平分线性质可以求得BA=BC,根据一个角为60°的等腰三角形为等边三角形即可解题.
(2)根据垂直平分线性质可以求得BA=BC,根据一个角为60°的等腰三角形为等边三角形即可解题.
解答:解:(1)∵AD∥BC,
∴∠ADE=∠CFE,∠DAE=∠FCE,
在△ADE和△CFE中,
,
∴△ADE≌△CFE(ASA),
∴DE=EF,
∴E是DF中点;
(2)∵△ADE≌△CFE,
∴AE=CE,
∵BE⊥AC,
∴DE是AC垂直平分线,
∴BA=BC,
∴△ABC是等腰三角形,
∵∠C=60°,
∴△ABC是等边三角形.
∴∠ADE=∠CFE,∠DAE=∠FCE,
在△ADE和△CFE中,
|
∴△ADE≌△CFE(ASA),
∴DE=EF,
∴E是DF中点;
(2)∵△ADE≌△CFE,
∴AE=CE,
∵BE⊥AC,
∴DE是AC垂直平分线,
∴BA=BC,
∴△ABC是等腰三角形,
∵∠C=60°,
∴△ABC是等边三角形.
点评:本题考查了全等三角形的判定,考查了全等三角形对应边相等的性质,考查了等边三角形的判定,本题中求证△ADE≌△CFE是解题的关键.

练习册系列答案
相关题目
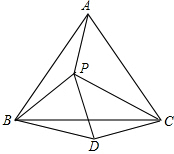 已知:如图,点P是等边△ABC内的一点,连结PA,PB,PC,以BP为边作等边△BPD,连结CD.
已知:如图,点P是等边△ABC内的一点,连结PA,PB,PC,以BP为边作等边△BPD,连结CD. 如图,在△ABC中,∠A=30°,∠B-∠C=60°,BC=2,求AC的长.
如图,在△ABC中,∠A=30°,∠B-∠C=60°,BC=2,求AC的长.