题目内容
 如图,在△ABC中,∠A=30°,∠B-∠C=60°,BC=2,求AC的长.
如图,在△ABC中,∠A=30°,∠B-∠C=60°,BC=2,求AC的长.考点:解直角三角形的应用
专题:
分析:由于△ABC为一般三角形,求AC的长,可通过作辅助线AC边的高BD,求出AD和CD的长,两者相加即可求出AC的长.
解答: 解:作AC边的高BD交AC于D,
解:作AC边的高BD交AC于D,
由∠A=30°可列:
,
解得:∠B=105°,∠C=45°,
在Rt△ABD中,由∠A=30°,可得:∠ABD=60°,∠CBD=45°,
在Rt△BCD中,由BC=2,可得BD=CD=tan45°×BC=
,
在Rt△ABD中,AD=tan60°×BD=
,
故AC=AD+BD=
+
.
 解:作AC边的高BD交AC于D,
解:作AC边的高BD交AC于D,由∠A=30°可列:
|
解得:∠B=105°,∠C=45°,
在Rt△ABD中,由∠A=30°,可得:∠ABD=60°,∠CBD=45°,
在Rt△BCD中,由BC=2,可得BD=CD=tan45°×BC=
| 2 |
在Rt△ABD中,AD=tan60°×BD=
| 6 |
故AC=AD+BD=
| 6 |
| 2 |
点评:考查了解直角三角形的应用,本题通过作辅助线可使边的求解更为简单,在计算过程中应注意对三角函数的应用.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
甲数比乙数的3倍大2,若设乙数为x,则甲数为( )
| A、3x-2 | ||
B、3x-
| ||
C、
| ||
| D、3x+2 |
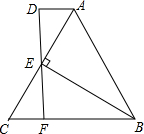 如图,已知△ABC,过A点作过AD∥BC,DF和AC交于E点,且AD=CF,连BE
如图,已知△ABC,过A点作过AD∥BC,DF和AC交于E点,且AD=CF,连BE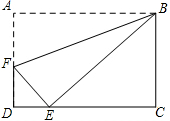 如图,在矩形ABCD中,AB:BC=2:
如图,在矩形ABCD中,AB:BC=2: