题目内容
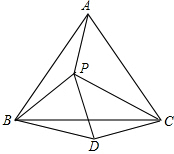 已知:如图,点P是等边△ABC内的一点,连结PA,PB,PC,以BP为边作等边△BPD,连结CD.
已知:如图,点P是等边△ABC内的一点,连结PA,PB,PC,以BP为边作等边△BPD,连结CD.(1)猜想AP与CD之间的大小关系,并证明.
(2)若∠APB=150°,PD=10,CD=15,求△PDC的面积.
考点:全等三角形的判定与性质,等边三角形的性质
专题:
分析:(1)易证∠ABP=∠CBD,即可求证△ABP≌△CBD,即可求得AP=CD;
(2)根据(1)可得∠BDC=∠APB,再根据∠BDC可以求得∠PDC的大小,即可解题.
(2)根据(1)可得∠BDC=∠APB,再根据∠BDC可以求得∠PDC的大小,即可解题.
解答:解:(1)∵∠ABC=∠PBD=60°,
∴∠ABP=∠CBD,
在△ABP和△CBD中,
,
∴△ABP≌△CBD(SAS),
∴AP=CD;
(2)∵△ABP≌△CBD,
∴∠BDC=∠APB=150°,
∵∠BDC=∠BDP+∠PDC,
∴∠PDC=150°-60°=90°,
∴△PDC的面积S=
PD•DC=75.
∴∠ABP=∠CBD,
在△ABP和△CBD中,
|
∴△ABP≌△CBD(SAS),
∴AP=CD;
(2)∵△ABP≌△CBD,
∴∠BDC=∠APB=150°,
∵∠BDC=∠BDP+∠PDC,
∴∠PDC=150°-60°=90°,
∴△PDC的面积S=
| 1 |
| 2 |
点评:本题考查了全等三角形的判定,考查了全等三角形对应角相等的性质,本题中求证△ABP≌△CBD是解题的关键.

练习册系列答案
相关题目
 实数a,b,c在数轴上的对应点的位置如图所示,化简|a-b|+|a-c|-|b-c|的结果.
实数a,b,c在数轴上的对应点的位置如图所示,化简|a-b|+|a-c|-|b-c|的结果. 已知a、b两数在数轴上的表示如图所示,化简:
已知a、b两数在数轴上的表示如图所示,化简: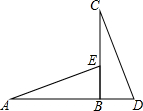 如图,BC⊥AD于点B,AB=BC,点E在线段BC上,BE=BD,连结AE,CD.
如图,BC⊥AD于点B,AB=BC,点E在线段BC上,BE=BD,连结AE,CD.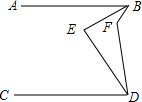 如图,AB∥CD,BE平分∠ABF,DE平分∠CDF,∠BFD=120°,求∠BED.
如图,AB∥CD,BE平分∠ABF,DE平分∠CDF,∠BFD=120°,求∠BED.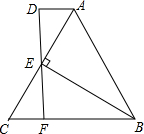 如图,已知△ABC,过A点作过AD∥BC,DF和AC交于E点,且AD=CF,连BE
如图,已知△ABC,过A点作过AD∥BC,DF和AC交于E点,且AD=CF,连BE