题目内容
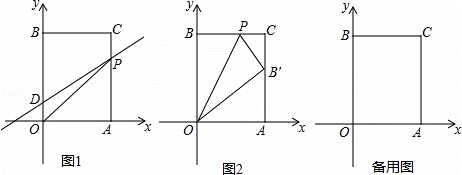
如图,在平面直角坐标系中,O是坐标原点,长方形OACB的顶点A、B分别在x轴与y轴上,已知A点坐标为(a,0),B点坐标为(0,b),且a,b满足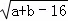 +|2a﹣b﹣2|=0.D为y轴上一点,其坐标为(0,2),点P从点A出发以每秒1个单位的速度沿线段AC﹣CB的方向运动,当点P与点B重合时停止运动,运动时间为t秒.
+|2a﹣b﹣2|=0.D为y轴上一点,其坐标为(0,2),点P从点A出发以每秒1个单位的速度沿线段AC﹣CB的方向运动,当点P与点B重合时停止运动,运动时间为t秒.
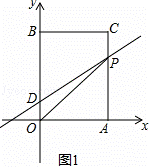
(1)当点P经过点C时,求直线DP的函数解析式;
(2)①求△OPD的面积S关于t的函数解析式;
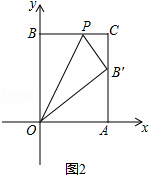
②如图②,把长方形沿着OP折叠,点B的对应点B′恰好落在AC边上,求点P的坐标.
(3)点P在运动过程中是否存在使△BDP为等腰三角形?若存在,请求出点P的坐标;若不存在,请说明理由.
解:(1)∵a,b满足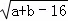 +|2a﹣b﹣2|=0,
+|2a﹣b﹣2|=0,
∴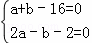 ,解得
,解得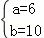 ,
,
∴点坐标为(6,0),B点坐标为(0,10),
∴C(6,10),
设此时直线DP解析式为y=kx+b,如图1,
将D(0,2),C(6,10)代入得: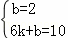 ,
,
解得: ,
,
则此时直线DP解析式为y=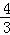 x+2;
x+2;
(2)①当点P在线段AC上时,OD=2,高为6,S=6;
当点P在线段BC上时,OD=2,高为6+10﹣t=16﹣t,S=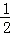 ×2×(16﹣t)=﹣t+16;
×2×(16﹣t)=﹣t+16;
②设P(m,10),则PB=PB′=m,如图2,
∵OB′=OB=10,OA=6,
∴AB′=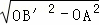 =8,
=8,
∴B′C=10﹣8=2,
∵PC=6﹣m,
∴m2=22+(6﹣m)2,解得m=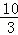
则此时点P的坐标是(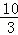 ,10);
,10);
(3)存在,理由为:
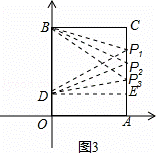
若△BDP为等腰三角形,分三种情况考虑:如图3,
①当BD=BP1=OB﹣OD=10﹣2=8,
在Rt△BCP1中,BP1=8,BC=6,
根据勾股定理得:CP1=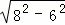 =2
=2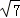 ,
,
∴AP1=10﹣2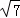 ,即P1(6,10﹣2
,即P1(6,10﹣2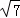 );
);
②当BP2=DP2时,此时P2(6,6);
③当DB=DP3=8时,
在Rt△DEP3中,DE=6,
根据勾股定理得:P3E=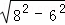 =2
=2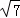 ,
,
∴AP3=AE+EP3=2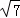 +2,即P3(6,2
+2,即P3(6,2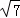 +2),
+2),
综上,满足题意的P坐标为(6,6)或(6,2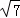 +2)或(6,10﹣2
+2)或(6,10﹣2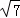 ).
).

 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案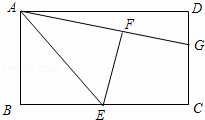

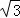 ﹣1)2+(
﹣1)2+(