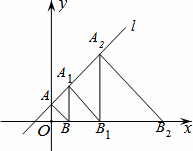题目内容
二次函数y=ax2+bx+c的图象如图所示,则下列结论①abc<0,②b2﹣4ac>0,③2a+b>0,④a+b+c<0,⑤ax2+bx+c+2=0的解为x=﹣0,其中正确的有( )个.
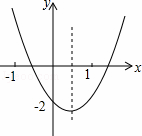
A. 2 B. 3 C. 4 D. 5
B 解:∵抛物线开口向上,对称轴在y轴右侧,且抛物线与y轴交于负半轴,
∴a>0,b<0,c<0,
∴abc>0,故选项①错误;
∵抛物线与x轴有两个交点,
∴b2﹣4ac>0,故选项②正确;
∵对称轴为直线x=﹣ <1,且a>0,
<1,且a>0,
∴2a+b>0,故选项③正确;
由图象可得:当x=1时,对应的函数图象上的点在x轴下方,
∴将x=1代入得:y=a+b+c<0,故选项④正确;
由图象可得:方程ax2+bx+c=﹣2有两解,其中一个为x=0,故选项⑤错误 ,
,
综上,正确的选项有:②③④共3个.
故选B.

练习册系列答案
相关题目
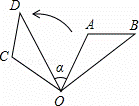
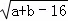 +|2a﹣b﹣2|=0.D为y轴上一点,其坐标为(0,2),点P从点A出发以每秒1个单位的速度沿线段AC﹣CB的方向运动,当点P与点B重合时停止运动,运动时间为t秒.
+|2a﹣b﹣2|=0.D为y轴上一点,其坐标为(0,2),点P从点A出发以每秒1个单位的速度沿线段AC﹣CB的方向运动,当点P与点B重合时停止运动,运动时间为t秒.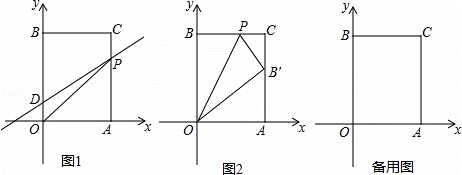



 Rt△A1BB1交直线l于点A1,再过B1点再作等腰Rt△A2B1B2交直线l于点A2,以此类推,继续作等腰Rt△A3B2B3﹣﹣﹣,Rt△AnBn﹣1Bn,其中点A0A1A2…An都在直线l上,点B0B1B2…Bn都在x轴上,且∠A1BB1,∠A2B1B2,∠A3B2B3…∠An﹣1BnBn﹣1都为直角.则点A3的坐标为 ,点An的坐标为 .
Rt△A1BB1交直线l于点A1,再过B1点再作等腰Rt△A2B1B2交直线l于点A2,以此类推,继续作等腰Rt△A3B2B3﹣﹣﹣,Rt△AnBn﹣1Bn,其中点A0A1A2…An都在直线l上,点B0B1B2…Bn都在x轴上,且∠A1BB1,∠A2B1B2,∠A3B2B3…∠An﹣1BnBn﹣1都为直角.则点A3的坐标为 ,点An的坐标为 .