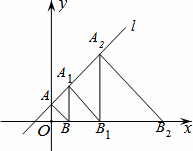题目内容
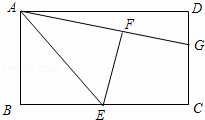
如图,在矩形ABCD中,E是BC的中点,将△ABE沿AE折叠后得到△AFE,点F在矩形ABCD内部,延长AF交CD于点G.
(1)猜想线段GF与GC有何数量关系?并证明你的结论;
(2)若AB=3,AD=4,求线段GC的长.
解:(1)GF=GC.
理由如下:连接GE,
∵E是BC的中点,
∴BE=EC,
∵△ABE沿AE折叠后得到△AFE,
∴BE=EF,
∴EF=EC,
∵在矩形ABCD中,
∴∠C=90°,
∴∠EFG=90°,
∵在Rt△GFE和Rt△GCE中,
 ,
,
∴Rt△GFE≌Rt△GCE(HL),
∴GF=GC;
(2)设GC=x,则AG=3+x,DG=3﹣x,
在Rt△ADG中,42+(3﹣x)2=(3+x)2,
解得x= .
.


练习册系列答案
相关题目
 +3
+3 =5
=5 B. 2
B. 2 =5
=5 C.
C.  =±4 D.
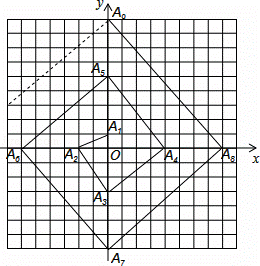
=±4 D.  ÷
÷
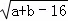 +|2a﹣b﹣2|=0.D为y轴上一点,其坐标为(0,2),点P从点A出发以每秒1个单位的速度沿线段AC﹣CB的方向运动,当点P与点B重合时停止运动,运动时间为t秒.
+|2a﹣b﹣2|=0.D为y轴上一点,其坐标为(0,2),点P从点A出发以每秒1个单位的速度沿线段AC﹣CB的方向运动,当点P与点B重合时停止运动,运动时间为t秒.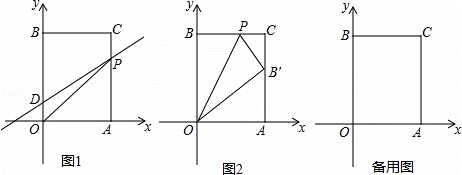
 Rt△A1BB1交直线l于点A1,再过B1点再作等腰Rt△A2B1B2交直线l于点A2,以此类推,继续作等腰Rt△A3B2B3﹣﹣﹣,Rt△AnBn﹣1Bn,其中点A0A1A2…An都在直线l上,点B0B1B2…Bn都在x轴上,且∠A1BB1,∠A2B1B2,∠A3B2B3…∠An﹣1BnBn﹣1都为直角.则点A3的坐标为 ,点An的坐标为 .
Rt△A1BB1交直线l于点A1,再过B1点再作等腰Rt△A2B1B2交直线l于点A2,以此类推,继续作等腰Rt△A3B2B3﹣﹣﹣,Rt△AnBn﹣1Bn,其中点A0A1A2…An都在直线l上,点B0B1B2…Bn都在x轴上,且∠A1BB1,∠A2B1B2,∠A3B2B3…∠An﹣1BnBn﹣1都为直角.则点A3的坐标为 ,点An的坐标为 .