题目内容
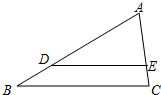如图，在△ABC中，点D、E分别在AB、AC边上，DE∥BC，若AD：AB=3：4，则S△ADE：S△ABC等于（ ）| A、3：4 | B、9：16 |
| C、6：8 | D、不能确定 |
考点：相似三角形的判定与性质
专题：
分析：由平行可得△ADE∽△ABC，根据相似比，利用相似三角形的性质可求得答案．
解答：解：∵DE∥BC，
∴△ADE∽△ABC，
∴
=（
）2=（
）2=
，
故选B．
∴△ADE∽△ABC，
∴
| S△ADE |
| S△ABC |
| AD |
| AB |
| 3 |
| 4 |
| 9 |
| 16 |
故选B．
点评：本题主要考查相似三角形的判定和性质，掌握相似三角形的面积比等于相似比的平方是解题的关键．
练习册系列答案
考前必练系列答案
相关题目
如图，抛物线y=（x-m）2-1（m＞0）与x轴交于A、B两点，若将该抛物线向左平移3个单位后恰好经过原点，求m的值．
如图，在?ABCD中，过点A作AE⊥BC．垂足为E，连结DE，F为线段DE上的一点，且∠AFE=∠B．
在正方形ABCD中，AB=4，O为AC的中点，点P在AC上，PF⊥CD垂足为F．连接PB．PE⊥PB，交直线DC于点E．设AP=x，△CPE的面积为y，求y与x的函数关系式．