题目内容
 如图,抛物线y=(x-m)2-1(m>0)与x轴交于A、B两点,若将该抛物线向左平移3个单位后恰好经过原点,求m的值.
如图,抛物线y=(x-m)2-1(m>0)与x轴交于A、B两点,若将该抛物线向左平移3个单位后恰好经过原点,求m的值.考点:二次函数图象与几何变换
专题:
分析:根据题意表示出平移后解析式,进而利用图象经过原点进而求出即可.
解答:解:∵抛物线y=(x-m)2-1(m>0)与x轴交于A、B两点,将该抛物线向左平移3个单位后,
∴平移后解析式为:y=(x-m+3)2-1,
∵平移后解析式恰好经过原点,
∴y=x2+2(3-m)x+(3-m)2-1过(0,0)点,
即(3-m)2-1=0,
解得:m1=2,m2=4,
∴平移后解析式为:y=(x-m+3)2-1,
∵平移后解析式恰好经过原点,
∴y=x2+2(3-m)x+(3-m)2-1过(0,0)点,
即(3-m)2-1=0,
解得:m1=2,m2=4,
点评:此题主要考查了二次函数图象与几何变换,表示出平移后解析式是解题关键.

练习册系列答案
相关题目
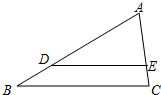 如图,在△ABC中,点D、E分别在AB、AC边上,DE∥BC,若AD:AB=3:4,则S△ADE:S△ABC等于( )
如图,在△ABC中,点D、E分别在AB、AC边上,DE∥BC,若AD:AB=3:4,则S△ADE:S△ABC等于( )| A、3:4 | B、9:16 |
| C、6:8 | D、不能确定 |
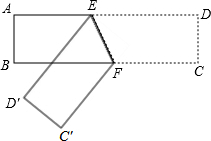 如图,一长方形纸片ABCD沿折痕EF对折,得到点D的对应点D′,点C的对应点C′,若∠BFE=50°,试求∠BFC′的度数.
如图,一长方形纸片ABCD沿折痕EF对折,得到点D的对应点D′,点C的对应点C′,若∠BFE=50°,试求∠BFC′的度数.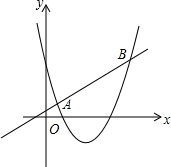 已知关于x的二次函数y=x2-2mx+m2+m的图象与关于x的函数y=x+1的图象交于两点A(x1,y1)、B(x2,y2);(x1<x2),m为任何值时,猜想AB的长是否不变?并证明你的猜想.
已知关于x的二次函数y=x2-2mx+m2+m的图象与关于x的函数y=x+1的图象交于两点A(x1,y1)、B(x2,y2);(x1<x2),m为任何值时,猜想AB的长是否不变?并证明你的猜想. 如图,
如图, 如图,梯形ABCD中,AB∥CD,∠B=90°,E为BC上一点,且∠AED=90°,若AB=5,BC=12,CD=7,求BE的长.
如图,梯形ABCD中,AB∥CD,∠B=90°,E为BC上一点,且∠AED=90°,若AB=5,BC=12,CD=7,求BE的长.