题目内容
 如图,在?ABCD中,过点A作AE⊥BC.垂足为E,连结DE,F为线段DE上的一点,且∠AFE=∠B.
如图,在?ABCD中,过点A作AE⊥BC.垂足为E,连结DE,F为线段DE上的一点,且∠AFE=∠B.(1)求证:AD•EC=DF•DE;
(2)AB=4,AD=3
| 3 |
考点:相似三角形的判定与性质
专题:
分析:(1)证明∠DAF=∠EDC,∠ADF=∠CED,进而得到△ADF∽△DEC,列出比例式化为等积式,即可解决问题.
(2)求出DE的长度;运用△ADF∽△DEC,列出比例式,即可解决问题.
(2)求出DE的长度;运用△ADF∽△DEC,列出比例式,即可解决问题.
解答: 解:(1)∵四边形ABCD是平行四边形,
解:(1)∵四边形ABCD是平行四边形,
∴∠ADC=∠B,AD∥BC;而∠AFE=∠B,
∴∠ADF=∠CED,∠AFE=∠ADC;
∵∠AFE=∠FAD+∠ADF,∠ADC=∠ADF+∠EDC,
∴∠DAF=∠EDC,而∠ADF=∠CED,
∴△ADF∽△DEC,
∴AD:DE=DF:EC,
∴AD•EC=DE•DF.
(2)∵AD∥BC,AE⊥BC,
∴AE⊥AD,
由勾股定理得:DE2=AD2+AE2,
而AD=3
,AE=3,
∴DE=6;
∵△ADF∽△DEC,
∴AD:DE=AF:DC,而DC=AB=4,
∴AF=2
.
 解:(1)∵四边形ABCD是平行四边形,
解:(1)∵四边形ABCD是平行四边形,∴∠ADC=∠B,AD∥BC;而∠AFE=∠B,
∴∠ADF=∠CED,∠AFE=∠ADC;
∵∠AFE=∠FAD+∠ADF,∠ADC=∠ADF+∠EDC,
∴∠DAF=∠EDC,而∠ADF=∠CED,
∴△ADF∽△DEC,
∴AD:DE=DF:EC,
∴AD•EC=DE•DF.
(2)∵AD∥BC,AE⊥BC,
∴AE⊥AD,
由勾股定理得:DE2=AD2+AE2,
而AD=3
| 3 |
∴DE=6;
∵△ADF∽△DEC,
∴AD:DE=AF:DC,而DC=AB=4,
∴AF=2
| 3 |
点评:该题主要考查了相似三角形的判定及其性质的应用问题;解题的关键是灵活运用有关定理来分析、判断、推理或解答.

练习册系列答案
 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
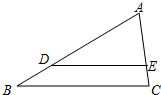 如图,在△ABC中,点D、E分别在AB、AC边上,DE∥BC,若AD:AB=3:4,则S△ADE:S△ABC等于( )
如图,在△ABC中,点D、E分别在AB、AC边上,DE∥BC,若AD:AB=3:4,则S△ADE:S△ABC等于( )| A、3:4 | B、9:16 |
| C、6:8 | D、不能确定 |
 如图,
如图, 实数a,b在数轴上的位置如图所示,化简
实数a,b在数轴上的位置如图所示,化简