题目内容
 在正方形ABCD中,AB=4,O为AC的中点,点P在AC上,PF⊥CD垂足为F.连接PB.PE⊥PB,交直线DC于点E.设AP=x,△CPE的面积为y,求y与x的函数关系式.
在正方形ABCD中,AB=4,O为AC的中点,点P在AC上,PF⊥CD垂足为F.连接PB.PE⊥PB,交直线DC于点E.设AP=x,△CPE的面积为y,求y与x的函数关系式.考点:正方形的性质,全等三角形的判定与性质
专题:
分析:延长FP交AB于G,判断出△APG是等腰直角三角形,根据等腰直角三角形的性质可得AG=PG,然后求出BG=PF,再求出∠PBG=∠EPF,然后利用“角边角”证明△PBG和△EPF全等,根据全等三角形对应边相等可得EF=PG,再求出PG,表示出CE,然后利用三角形的面积公式列式整理即可得解.
解答: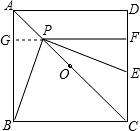 解:如图,延长FP交AB于G,
解:如图,延长FP交AB于G,
∵四边形ABCD是正方形,
∴∠BAC=45°,
∵PF⊥CD,
∴PG⊥AB,
∴△APG是等腰直角三角形,
∴AG=PG,
∴AB-AG=GF-PG,
即BG=PF,
∵PE⊥PB,
∴∠PBG+∠BPG=∠EPF+∠BPG=90°,
∴∠PBG=∠EPF,
在△PBG和△EPF中,
,
∴△PBG≌△EPF(ASA),
∴EF=PG,
∵AP=x,
∴PG=
x,
∴CE=4-2×
x=4-
x,
又∵PF=4-
x,
∴△CPE的面积为y=
×(4-
x)×(4-
x)=
x2-3
x+8,
即y=
x2-3
x+8.
 解:如图,延长FP交AB于G,
解:如图,延长FP交AB于G,∵四边形ABCD是正方形,
∴∠BAC=45°,
∵PF⊥CD,
∴PG⊥AB,
∴△APG是等腰直角三角形,
∴AG=PG,
∴AB-AG=GF-PG,
即BG=PF,
∵PE⊥PB,
∴∠PBG+∠BPG=∠EPF+∠BPG=90°,
∴∠PBG=∠EPF,
在△PBG和△EPF中,
|
∴△PBG≌△EPF(ASA),
∴EF=PG,
∵AP=x,
∴PG=
| ||
| 2 |
∴CE=4-2×
| ||
| 2 |
| 2 |
又∵PF=4-
| ||
| 2 |
∴△CPE的面积为y=
| 1 |
| 2 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| 2 |
即y=
| 1 |
| 2 |
| 2 |
点评:本题考查了正方形的性质,全等三角形的判定与性质,等腰直角三角形的判定与性质,熟记各性质并作辅助线构造出全等三角形是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
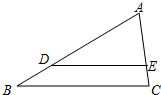 如图,在△ABC中,点D、E分别在AB、AC边上,DE∥BC,若AD:AB=3:4,则S△ADE:S△ABC等于( )
如图,在△ABC中,点D、E分别在AB、AC边上,DE∥BC,若AD:AB=3:4,则S△ADE:S△ABC等于( )| A、3:4 | B、9:16 |
| C、6:8 | D、不能确定 |
 如图,梯形ABCD中,AB∥CD,∠B=90°,E为BC上一点,且∠AED=90°,若AB=5,BC=12,CD=7,求BE的长.
如图,梯形ABCD中,AB∥CD,∠B=90°,E为BC上一点,且∠AED=90°,若AB=5,BC=12,CD=7,求BE的长. 我们知道平行四边形的两条对角线把平行四边形分成了四个面积相等的小三角形,如图,若O为平行四边形对角线AC上任意一点(不包括A,C)那么图中分成的四个小三角形的面积还相等吗?若相等,说明理由;若不相等,你能说出它们之间还存在什么关系吗?为什么?
我们知道平行四边形的两条对角线把平行四边形分成了四个面积相等的小三角形,如图,若O为平行四边形对角线AC上任意一点(不包括A,C)那么图中分成的四个小三角形的面积还相等吗?若相等,说明理由;若不相等,你能说出它们之间还存在什么关系吗?为什么?