题目内容
16. 如图,已知函数y=x+b和y=ax+3图象的交点为P,则方程x+b=ax+3的解为x=1,不等式x+b>ax+3的解集是x>1,不等式x+b<ax+3的解集是x<1.
如图,已知函数y=x+b和y=ax+3图象的交点为P,则方程x+b=ax+3的解为x=1,不等式x+b>ax+3的解集是x>1,不等式x+b<ax+3的解集是x<1.
分析 利用两函数图象的交点问题得到当x=1时,x+b=ax+3;观察函数图象,找出直线y=kx+b在直线y=ax+3上方所对应的自变量的范围和直线y=kx+b在直线y=ax+3下方所对应的自变量的范围即可得到两不等式的解集.
解答 解:∵函数y=x+b和y=ax+3的图象的交点为P的横坐标为1,
∴方程x+b=ax+3的解为x=1;
当x>1时,x+b>ax+3;当x<1时,x+b<ax+3.
故答案为x=1,x>1,x<1.
点评 本题考查了一次函数与一元一次不等式:一次函数与一元一次不等式的关系从函数的角度看,就是寻求使一次函数y=kx+b的值大于(或小于)0的自变量x的取值范围;从函数图象的角度看,就是确定直线y=kx+b在x轴上(或下)方部分所有的点的横坐标所构成的集合.

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
7.在坐标系中,以原点为圆心,以5为半径画圆,则点A(-3,4)的在( )
| A. | 圆内 | B. | 圆上 | C. | 圆外 | D. | 不能确定 |
5.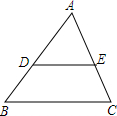 如图,在△ABC中,D、E分别在AB、AC上,DE∥BC,且AD:DB=3:2,则S△ADE:S四边形DECB为( )
如图,在△ABC中,D、E分别在AB、AC上,DE∥BC,且AD:DB=3:2,则S△ADE:S四边形DECB为( )
 如图,在△ABC中,D、E分别在AB、AC上,DE∥BC,且AD:DB=3:2,则S△ADE:S四边形DECB为( )
如图,在△ABC中,D、E分别在AB、AC上,DE∥BC,且AD:DB=3:2,则S△ADE:S四边形DECB为( )| A. | 3:2 | B. | 3:5 | C. | 9:25 | D. | 9:16 |
 如图,小明要用54m的篱笆靠墙围成一个面积为300m2的长方形场地,在与墙平行的一边留一道1m宽的门,已知墙长为20m,求这块场地两邻边的长.
如图,小明要用54m的篱笆靠墙围成一个面积为300m2的长方形场地,在与墙平行的一边留一道1m宽的门,已知墙长为20m,求这块场地两邻边的长.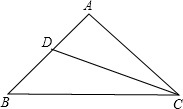 如图,△ABC中,∠A=90°,CD平分∠ACB,若AD=1,AC=2,BC=$\frac{10}{3}$,求△ABC的面积.
如图,△ABC中,∠A=90°,CD平分∠ACB,若AD=1,AC=2,BC=$\frac{10}{3}$,求△ABC的面积.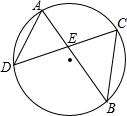 如图,AD=BC,求证:AB=DC,BE=DE.
如图,AD=BC,求证:AB=DC,BE=DE.