题目内容
若M(-
,y1)、N(-
,y2)、P(
,y3)三点都在函数y=-
(k>0)的图象上,则y1、y2、y3的大小关系是 .
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
| 2 |
| x |
考点:反比例函数图象上点的坐标特征
专题:计算题
分析:根据反比例函数图象上点的坐标特征得到-
•y1=-2,-
•y2=-2,
•y3=-2,然后解方程求出y1,y2,y3,再比较它们的大小.
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
解答:解:根据题意得-
•y1=-2,-
•y2=-2,
•y3=-2,
解得y1=4,y2=8,
•y3=-4,
所以y3<y1<y2.
故答案为y3<y1<y2.
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
解得y1=4,y2=8,
| 1 |
| 2 |
所以y3<y1<y2.
故答案为y3<y1<y2.
点评:本题考查了反比例函数图象上点的坐标特征:反比例函数y=
(k为常数,k≠0)的图象是双曲线,图象上的点(x,y)的横纵坐标的积是定值k,即xy=k.
| k |
| x |

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
无论x取何值时,下列分式中总有意义的是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
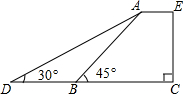 如图是某滑板俱乐部训练时的斜坡截面的示意图,该截面垂直于水平面,出于安全因素考虑,俱乐部决定将训练的斜坡AB改造成AD,这时斜坡的坡角由45°降为30°,已知原斜坡面AB的长为6米,点D,B,C在同一水平直线上,AE∥DC,改善后斜坡坡面AD的长为多少米?
如图是某滑板俱乐部训练时的斜坡截面的示意图,该截面垂直于水平面,出于安全因素考虑,俱乐部决定将训练的斜坡AB改造成AD,这时斜坡的坡角由45°降为30°,已知原斜坡面AB的长为6米,点D,B,C在同一水平直线上,AE∥DC,改善后斜坡坡面AD的长为多少米? 如图,△ABC中,∠C=90°,AC=3,BC=4,AB的垂直平分线交AB于E,交BC于D,则BD的长为
如图,△ABC中,∠C=90°,AC=3,BC=4,AB的垂直平分线交AB于E,交BC于D,则BD的长为