题目内容
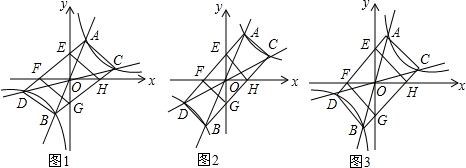
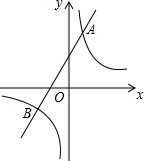
17.如图1,直线y=k1x与反比例函数y=$\frac{k}{x}$(k≠0)的图象交于点A,B,直线y=k2x与反比例函数y=$\frac{k}{x}$的图象交于点C,D,且k1•k2≠0,k1≠k2,顺次连接A,D,B,C,AD,BC分别交x轴于点F,H,交y轴于点E,G,连接FG,EH.(1)四边形ADBC的形状是平行四边形;
(2)如图2,若点A的坐标为(2,4),四边形AEHC是正方形,则k2=$\frac{1}{2}$;
(3)如图3,若四边形EFGH为正方形,点A的坐标为(2,6),求点C的坐标;
(4)判断:随着k1、k2取值的变化,四边形ADBC能否为正方形?若能,求点A的坐标;若不能,请简要说明理由.
分析 (1)直接根据正比例函数与反比例函数的性质即可得出结论;
(2)过点A作AM⊥y轴,垂足为M,过点C作CN⊥x轴,垂足为N,根据四边形AEHC是正方形可知OA=OC,故可得出△OAM≌△OCN,AM=CN,由此可得出C点坐标,由此可得出C点坐标,利用待定系数法求出k2的值即可;
(3)过点A作AM⊥y轴,垂足为M,过点C作CN⊥x轴,垂足为N,根据四边形EFGH为正方形可得出AM=AE.CN=HN.由点A(2,6)得出AM=ME=2,OM=6,设CN=HN=m,则点C的坐标为(4+m,m).根据反比例函数y=$\frac{k}{x}$的图象过点C和点A(2,6)可得出m的值,进而可得出结论;
(4)根据反比例函数y=$\frac{k}{x}$(k≠0)的图象不能与坐标轴相交可知∠AOC<90°,故四边形ADBC的对角线不能互相垂直,由此可得出结论.
解答  解:(1)∵正比例函数与反比例函数的图象均关于原点对称,
解:(1)∵正比例函数与反比例函数的图象均关于原点对称,
∴OA=OB,OC=OD,
∴四边形ADBC是平行四边形.
故答案为:平行四边形;
(2)如图1,过点A作AM⊥y轴,垂足为M,过点C作CN⊥x轴,垂足为N,
∵四边形AEHC是正方形,
∴DA⊥AC,
∴四边形ADBC是矩形,
∴OA=OC.
∴AM=CN,
∴C(4,2),
∴2=4k2,解得k2=$\frac{1}{2}$.
故答案为;$\frac{1}{2}$;
(3)如图2所示,过点A作AM⊥y轴,垂足为M,过点C作CN⊥x轴,垂足为N,
∵四边形EFGH为正方形,
∴∠FEO=45°,EO=HO,
∴∠AEM=45°.
∵∠AME=90°,
∴∠EAM=∠AEM=45°.
∴AM=EM.
同理,CN=HN.
∵点A(2,6),
∴AM=ME=2,OM=6,
∴OE=OH=4.
设CN=HN=m,则点C的坐标为(4+m,m).
∵反比例函数y=$\frac{k}{x}$的图象过点C和点A(2,6),
∴m•(4+m)=12,解得m1=2,m2=-6(舍去);
当m=2时,m+4=6,
∴点C的坐标为(6,2);
(4)不能.
∵反比例函数y=$\frac{k}{x}$(k≠0)的图象不能与坐标轴相交,
∴∠AOC<90°,
∴四边形ADBC的对角线不能互相垂直,
∴四边形ADBC不能是正方形.
点评 本题考查的是反比例函数综合题,涉及到反比例函数与正比例函数的性质、正方形的性质等知识,难度适中.

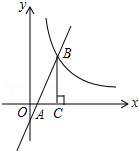 如图,一次函数y=kx-1的图象与x轴交于点A,与反比例函数y=$\frac{3}{x}$(x>0)的图象交于点B,BC垂直x轴于点C.若△ABC的面积为1,则k的值是( )
如图,一次函数y=kx-1的图象与x轴交于点A,与反比例函数y=$\frac{3}{x}$(x>0)的图象交于点B,BC垂直x轴于点C.若△ABC的面积为1,则k的值是( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
 已知实数a,b在数轴上的位置如图所示,下列结论错误的是( )
已知实数a,b在数轴上的位置如图所示,下列结论错误的是( )| A. | |a|<1<|b| | B. | 1<-a<b | C. | 1<|a|<b | D. | -b<a<-1 |
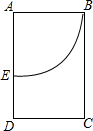 在长方形ABCD中AB=16,如图所示裁出一扇形ABE,将扇形围成一个圆锥(AB和AE重合),则此圆锥的底面半径为( )
在长方形ABCD中AB=16,如图所示裁出一扇形ABE,将扇形围成一个圆锥(AB和AE重合),则此圆锥的底面半径为( )| A. | 4 | B. | 16 | C. | 4$\sqrt{2}$ | D. | 8 |
 如图,直线a,b与直线c,d相交,已知∠1=∠2,∠3=110°,则∠4=( )
如图,直线a,b与直线c,d相交,已知∠1=∠2,∠3=110°,则∠4=( )| A. | 70° | B. | 80° | C. | 110° | D. | 100° |
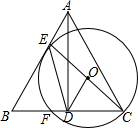 如图,在△ABC中,AB=AC,AD⊥BC于点D,E为边AB上一点,ED=CD,以CE为直径作⊙O,交BC于点F.
如图,在△ABC中,AB=AC,AD⊥BC于点D,E为边AB上一点,ED=CD,以CE为直径作⊙O,交BC于点F.
 如图,已知反比例函数y=$\frac{m}{x}$的图象与一次函数y=ax+b的图象相交于点A(1,4)和点B(n,-2).
如图,已知反比例函数y=$\frac{m}{x}$的图象与一次函数y=ax+b的图象相交于点A(1,4)和点B(n,-2).