题目内容
13. 如图,在四边形ABCD,AB⊥BC,AC⊥CD,AB=2,CD=8,tan∠BAC=2,求tanD的值.
如图,在四边形ABCD,AB⊥BC,AC⊥CD,AB=2,CD=8,tan∠BAC=2,求tanD的值.
分析 由已知条件得到∠B=∠ACD=90°,在Rt△ABC中,tan∠BAC=$\frac{BC}{AB}$=2,求得BC=4,根据勾股定理得到AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=2$\sqrt{5}$,于是得到结论.
解答 解:∵AB⊥BC,AC⊥CD,
∴∠B=∠ACD=90°,
在Rt△ABC中,tan∠BAC=$\frac{BC}{AB}$=2,
∵AB=2,
∴BC=4,
∴AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=2$\sqrt{5}$,
在Rt△ACD中,tan∠D=$\frac{AC}{CD}=\frac{2\sqrt{5}}{8}$=$\frac{\sqrt{5}}{4}$.
点评 本题考查了解直角三角形,勾股定理,熟练掌握锐角三角函数的定义是解题的关键.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
3.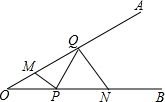 如图,∠AOB=30°,M,N分别是边OA,OB上的定点,P、Q分别是边OB,OA上的动点,记∠AMP=∠1,∠ONQ=∠2,当MP+PQ+QN最小时,则关于∠1,∠2的数量关系正确的是( )
如图,∠AOB=30°,M,N分别是边OA,OB上的定点,P、Q分别是边OB,OA上的动点,记∠AMP=∠1,∠ONQ=∠2,当MP+PQ+QN最小时,则关于∠1,∠2的数量关系正确的是( )
 如图,∠AOB=30°,M,N分别是边OA,OB上的定点,P、Q分别是边OB,OA上的动点,记∠AMP=∠1,∠ONQ=∠2,当MP+PQ+QN最小时,则关于∠1,∠2的数量关系正确的是( )
如图,∠AOB=30°,M,N分别是边OA,OB上的定点,P、Q分别是边OB,OA上的动点,记∠AMP=∠1,∠ONQ=∠2,当MP+PQ+QN最小时,则关于∠1,∠2的数量关系正确的是( )| A. | ∠1+∠2=90° | B. | 2∠2-∠1=30° | C. | 2∠1+∠2=180° | D. | ∠1-∠2=90° |
 如图,直线y1=k1x与y2=k2x+b相交于点A(3,4),且OA=OB,求:
如图,直线y1=k1x与y2=k2x+b相交于点A(3,4),且OA=OB,求: 如图,在l上找一点P,使|PA-PB|最大.
如图,在l上找一点P,使|PA-PB|最大.